Multiple Linear Regression - Prediction

Research Objective

Research Question: How well can we use the explanatory variables to predict height?

Population: All BYU students.

Parameters of Interest: The regression line parameters (all slopes and spread (\(\sigma\)))

Sample: A convenience sample of 1727 BYU students who are in Stat 121.

Research Objective

Research Question: What is the average height for male students who have a 64 inch tall mom, 68 inch tall dad, did not play sports in HS and wears a size 9 shoe?

Fitted Model: \[ \begin{align} \hat{y} &= 23.26 + 0.28\times \text{MotherHeight}_i + 0.21\times \text{FatherHeight}_i + 0.35\times \text{Sports}_i + \\ & \qquad 3.19\times \text{Sex}_i + 1.06\times \text{ShoeSize}_i \end{align} \] How would you use the model to figure this out?

Research Objective

Research Question: What is the average height for male students who have a 64 inch tall mom, 68 inch tall dad, did not play sports in HS and wears a size 9 shoe?

Fitted Model: \[ \begin{align} \hat{y} &= 23.26 + 0.28\times \text{MotherHeight}_i + 0.21\times \text{FatherHeight}_i + 0.35\times \text{Sports}_i + \\ & \qquad 3.19\times \text{Sex}_i + 1.06\times \text{ShoeSize}_i \end{align} \] How would you use the model to figure this out? \[ \begin{align} \hat{y} &= 23.26 + 0.28\times 64 + 0.21\times 68 + 0.35\times 0 + 3.19\times 1 + 1.06\times 9 \\ &= 68.419 \end{align} \]

Prediction in Regression

Thought Question: Is our prediction of \(\hat{y}\) = 68.419 of the average height for male students who have a 64 inch tall mom, 68 inch tall dad, did not play sports in HS and wears a size 9 shoe a sample estimate or population parameter?

  • Sample estimate!
  • We would rather build an interval for the population parameter.

Confidence Intervals for Averages

Using similar principles as we have used in the past to build confidence intervals: \[ \hat{y} \pm t^\star\text{SE}(\hat{\beta}_0 + \hat{\beta}_1\text{MH} + \cdots + \hat{\beta}_5\text{Shoe}) \] Is a confidence interval for the average value of \(y\) given an \(x\) (the population average height for male students who has a 64 inch tall mom, 68 inch tall dad, did not play sports in HS and wears a size 9) where the value of \(t^\star\) is determined by the confidence level.

For our analysis, this comes out to be (68.177, 68.665) for a 95% interval.

Notes:

  1. Don’t worry about the formula (computer will calculate this for you).
  2. Interpetation: We are 95% confident that the average height for all male students who has a 64 inch tall mom, 68 inch tall dad, did not play sports in HS and wears a size 9 is between 68.177 and 68.665.

Practice 7.3 Question 1

Remembering what we learned from simple linear regression, what is the difference between a prediction interval and a confidence interval in regression?

  1. A prediction interval is an interval for a single individual while a confidence interval is an interval for the average.
  2. A confidence interval is an interval for a single individual while a prediction interval is an interval for the average.
  3. There is no difference between the two.

Practice 7.3 Question 1 Answer

Remembering what we learned from simple linear regression, what is the difference between a prediction interval and a confidence interval in regression?

  1. A prediction interval is an interval for a single individual while a confidence interval is an interval for the average.
  2. A confidence interval is an interval for a single individual while a prediction interval is an interval for the average.
  3. There is no difference between the two.

Practice 7.3 Question 2

Remembering what we learned from simple linear regression, which interval is wider and why?

  1. A confidence interval is wider because there is more variability for averages than for individuals.
  2. A confidence interval is wider because there is more variability for individuals than for averages.
  3. A prediction interval is wider because there is more variability for averages than for individuals.
  4. A prediction interval is wider because there is more variability for individuals than for averages.

Practice 7.3 Question 2 Answer

Remembering what we learned from simple linear regression, which interval is wider and why?

  1. A confidence interval is wider because there is more variability for averages than for individuals.
  2. A confidence interval is wider because there is more variability for individuals than for averages.
  3. A prediction interval is wider because there is more variability for averages than for individuals.
  4. A prediction interval is wider because there is more variability for individuals than for averages.

Prediction Intervals for Individuals

Research Question: Eddie is a male student who has a 64 inch tall mom, 68 inch tall dad, did not play sports in HS and wears a size 9. What will his height be?

Using similar principles as we have used in the past to build confidence intervals: \[ \hat{y} \pm t^\star \text{SE}(\hat{\beta}_0 + \hat{\beta}_1\text{MH} + \cdots + \hat{\beta}_5\text{Shoe} + \hat{\epsilon}) \] is a prediction interval for the value of \(y\) given an \(x\) (for example, Eddie’s height) where the value of \(t^\star\) is determined by the confidence level.

For our analysis, this comes out to be (64.928, 71.914) for a 95% interval.

Notes:

  1. Don’t worry about the formula (computer will calculate this for you).
  2. Interpetation is similar: We are 95% confident that Eddie’s height will be between 64.928 and 71.914.

Prediction vs Confidence Intervals

Confidence interval for prediction: An interval estimate for the average of \(y\) given the \(x's\).

Prediction interval for prediction: An interval estimate for the value of a single \(y\) given the \(x's\).

  • Prediction intervals are ALWAYS wider than confidence intervals. Why?
  • There is more variability from student to student than the average of all students

Using the Analysis Tool

All of the steps are the same as in previous lectures…

Nuances of Predictions

Research Question: Jordan is a male student who has a 77 inch tall mom, 85 inch tall dad, did play sports in HS and wears a size 12 shoe. What will his height be?

Answer:

  • Don’t do the prediction because it’s outside of the data range! This is referred to as extrapolation.

Practice 7.3 Question 3

Hawaii is ocean bordering state with a latitude of 19.90 degrees and longitude of 155.67. What is a 90% interval for the melanoma mortality for this state? Enter -999 if doing this prediction is not appropriate.

Practice 7.3 Question 3 Answer

Hawaii is ocean bordering state with a latitude of 19.90 degrees and longitude of 155.67. What is a 90% interval for the melanoma mortality for this state? Enter -999 if doing this prediction is not appropriate.

  • -999 (this is outside the range of the data)

Nuances of Predictions

  1. Extrapolation - trying to predict outside of the range of the data.
  • In multiple linear regression, we have several ways to extrapolate. If ANY of the explanatory values are outside the range of the data, we shouldn’t do the prediction.

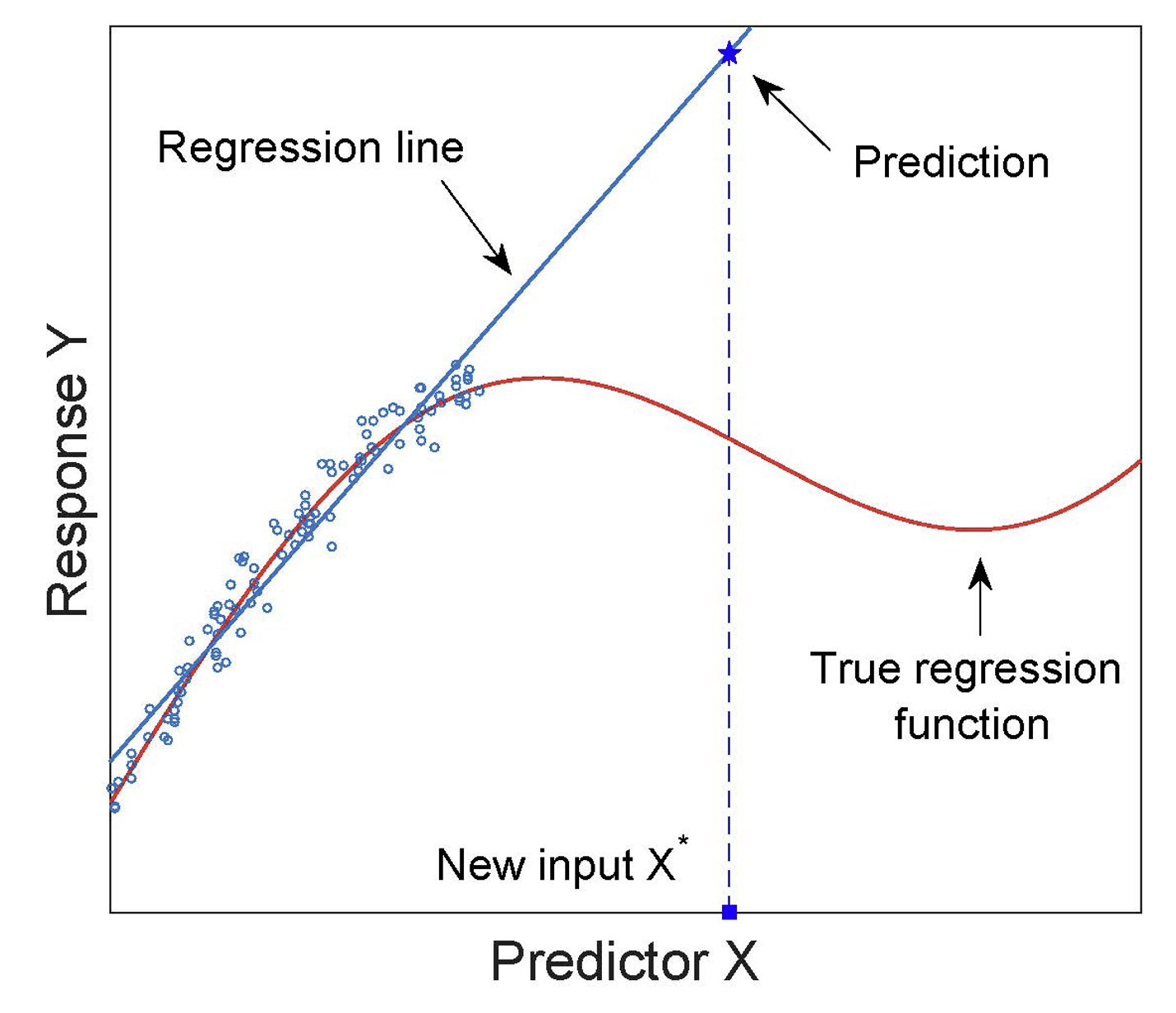
Practice Question 4

What method is used to determine if predictions from regression are accurate or not?

  1. Sampling distribution
  2. Hypothesis test
  3. Cross-validation
  4. Confidence interval

Practice Question 4 Answer

What method is used to determine if predictions from regression are accurate or not?

  1. Sampling distribution
  2. Hypothesis test
  3. Cross-validation
  4. Confidence interval

Nuances of Predictions

How do we know if our predictions are any good?

  • Use K-fold Cross Validation to see how well you are predicting.

Nuances of Predictions

Notes:

  1. Randomly split the data into validation folds. Each “fold” gets a turn to be predicted.
  2. Lots of performance metrics but most common is root mean square error \[ \text{RMSE} = \sqrt{\frac{1}{n_{\text{validation}}}\sum_{i=1}^{n_{\text{validation}}}(y_i - \hat{y}_i)^2} \] where \(y_i\) is an observation in the validation set and \(\hat{y}_i\) is the corresponding prediction.
  3. The intuitive interpretation of RMSE is the average error in our prediction.

Practice 7.3 Question 5

Model 1 uses just latitude to predict mortality and has a RMSE of 15. Model 2 uses latitude and ocean to predict mortality and has a RMSE of 14. Model 3 uses latitude, ocean and longitude to predict mortality and has an RMSE of 14.9. Which model is the preferred model to use?

  1. Model 1
  2. Model 2
  3. Model 3
  4. Cannot be determined from the given information

Practice 7.3 Question 5 Answer

Model 1 uses just latitude to predict mortality and has a RMSE of 15. Model 2 uses latitude and ocean to predict mortality and has a RMSE of 14. Model 3 uses latitude, ocean and longitude to predict mortality and has an RMSE of 14.9. Which model is the preferred model to use?

  1. Model 1
  2. Model 2 because it gives the lowest RMSE (prediction error)
  3. Model 3
  4. Cannot be determined from the given information

Additional Prediction Practice

Measuring possum head size can be difficult. However, various other factors can be used to predict head size? Use a multiple linear regression model (and the course app) to answer the following questions:

  1. Hyrum found a huge (96 cm total, male, 7 years, 68cm skull, 42 length tail) possum, What is your predicted head length for this possum?

    • 101.7571379 with a 95% prediction interval is (97.278, 106.237).

  2. Hyrum found a huge (96 cm total, male, 7 years, 68cm skull, 42 length tail) possum. What is the average head length for possums of this size?

    • 101.7571379 with 95% confidence interval is (100.021, 103.493).

  3. Hyrum found a baby (70 cm total, male, 0.5 years, 42cm skull, 28 length tail) possum. What is your predicted head length for this possum?

    • EXTRAPOLATION

  4. Is your model good or bad at possum head sizes?

    • The RMSE of a 10 fold CV is 1.6442366.

Key Terminology

  • Confidence Intervals for Averages
  • Extrapolation
  • Prediction Intervals for Individuals
  • Cross validation
  • Root mean square error (RMSE)