
Multiple Linear Regression - Inference
Research Objective
Research Question: What determines a person’s height?
Population: All BYU students.
Parameter of Interest:
- Some number measuring the “relationship” between height and various other explanatory variables such as fathers height, mother’s height, etc.
- For regression, these are the “slopes” or “effects” (e.g. \(\beta_1\)) in the model.
Sample: A convenience sample of 1727 BYU students who are in Stat 121.
Research Objective
Research Question: Is the height of a student influenced by any of the explanatory variables?
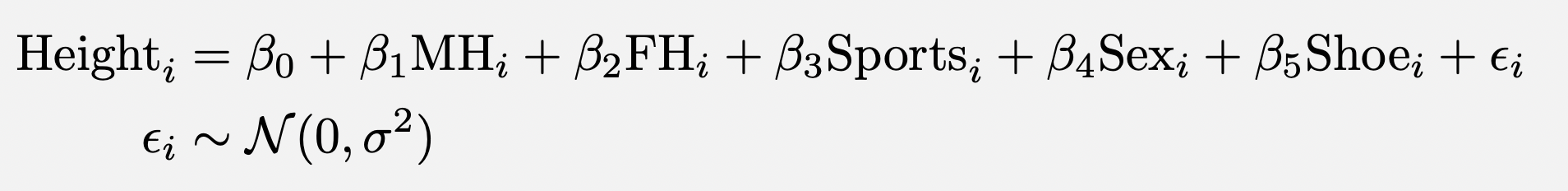
What would it mean if \(\beta_1 = \beta_2 = \cdots = \beta_5 = 0\)?
- There is no relationship between the student’s height (y) and ANY of the explanatory variables.
- This can be a useful hypothesis to test, particularly if you have a lot of explanatory variables.
Overall Hypothesis Testing in MLR
Research Question: Is the height of a student influenced by any of the explanatory variables?
Steps of hypothesis testing:
- Formulate null and alternative hypotheses.
- Gather the data and see if our sample data matches (or doesn’t match) the null hypothesis.
- Draw a conclusion about \(H_0\).
Overall Hypothesis Testing - Step 1
Research Question: Is the height of a student influenced by any of the explanatory variables?
Knowing what we did with other hypothesis tests, how would we write out our hypotheses? \[ \begin{align} H_0: & \\ H_a: & \end{align} \]
Overall Hypothesis Testing - Step 1
Research Question: Is the height of a student influenced by any of the explanatory variables?
Knowing what we did with other hypothesis tests, how would we write out our hypotheses? \[ \begin{align} H_0: & \beta_1 = \beta_2 = \beta_3 = \beta_4 = \beta_5 = 0\\ H_a: & \text{ At least one } \beta \text{ is not zero} \end{align} \]
Overall Hypothesis Testing - Step 2
Research Question: Is the height of a student influenced by any of the explanatory variables?
Step 2 - Compare our data result with what we expect to see if the null hypothesis is true.
- How do we do this?
- \(R^2\) will be key
- Recall that \(R^2\) is the percent of variability in the response explained by all the explanatory variables. So if \(R^2\) is close to 1 then the explanatory variables are doing a good job but \(R^2\) close to 0 means none of our explanatory variables are helpful.
Overall Hypothesis Testing - Step 2
Research Question: Is the height of a student influenced by any of the explanatory variables?
Step 2 - Compare our data result with what we expect to see if the null hypothesis is true.
\[ F = \frac{R^2/P}{(1-R^2)/(n-P-1)} \]
- If the null is true then \(F \approx 0\).
- We have \(F\) = 1443.941. Is this different enough from 0 to lead us to believe that \(H_0\) is false?
Overall Hypothesis Testing - Step 2
If the LINE assumptions of the regression model are appropriate, then \[ F = \frac{R^2/P}{(1-R^2)/(n-P-1)} \] is a test statistic and its sampling distribution follows an \(F\) distribution with degrees of freedom \(P\) and \(n-P-1\).
Overall Hypothesis Testing - Step 2
- So…what does that theorem mean?
- The \(F\)-distribution tells us what we should see in our sample if \(H_0\) is true
- The LINE assumptions about the population need to hold.
- The \(F\)-distribution tells us what we should see in our sample if \(H_0\) is true
Checking LINE Assumptions
Reminder, the LINE assumptions are:
- L - Linear relationship between QUANTITATIVE \(x\)’s and \(y\)
- I - Independence (one obs. doesn’t impact the other)
- N - Normal residuals (distance from line is normal)
- E - Equal variance of residuals (spread about the line is constant)
- How would we see if there is a linear relationship between \(x\)’s and \(y\)?
- Scatterplots work OK but can be deceiving because we have many \(x\)’s
- Added variable plots!
Checking LINE Assumptions

Are the relationships approximately linear?
Checking LINE Assumptions
How would we see if there is independence? In other words, how can we “check” if one observation doesn’t influence another?
- Critical Thinking!
- Does it “make sense” that one student’s height would be related to another student’s height?
- Maybe if there are relatives in the class but its likely a minimal influence.
Checking LINE Assumptions
How would we see if the residuals are normal?
- Calculate the residuals as \(\epsilon_i = y_i - (\hat{\beta}_0 + \hat{\beta}_1x_{1i} + \cdots + \hat{\beta}_5x_{5i})\) (don’t worry - the computer will do this for you)
- Draw a histogram (or density plot) of residuals
Checking LINE Assumptions
How would we see if the residuals are normal?
- Calculate the residuals as \(\epsilon_i = y_i - (\hat{\beta}_0 + \hat{\beta}_1x_{1i} + \cdots + \hat{\beta}_5x_{5i})\) (don’t worry - the computer will do this for you)
- Draw a histogram (or density plot) of residuals

Is this approximately normal?
- Skewness = 0.1193634
Checking LINE Assumptions
How would we see if there is “equal spread” of the residuals about the fitted line?
Checking LINE Assumptions
How would we see if there is “equal spread” of the residuals about the fitted line?
- Fitted values vs. residuals plot

Is this roughly “equal spread”?
- Yes except for a few outliers
Overall Hypothesis Tests in MLR
Research Question: Is the height of a student influenced by any of the explanatory variables?
Step 2 - Measuring if our data is consistent with the null hypothesis:
- The LINE assumptions are met so we can use the \(F\)-distribution to do our overall hypothesis test (also called an omnibus test).
Overall Hypothesis Tests in MLR
Research Question: Is the height of a student influenced by any of the explanatory variables?
Step 2 - Measuring if our data is consistent with the null hypothesis:
- Test statistic: In our height example \(F =\) 1443.941 (it should be 0 if \(H_0\) is true).
- \(p\)-value: probability of observing our sample result or “more extreme” (as stated by \(H_a\)) if the null hypothesis is true. Our \(p\)-value is 0.
Step 3: Draw a conclusions about \(H_0: \beta_1=\cdots=\beta_5=0\). Using \(\alpha = 0.05\), what do we conclude?
- Our data is NOT consistent with the null hypothesis so we conclude that at least 1 explanatory variable does have an effect on height.
- If we reject, this is a painfully vague conclusion. We need to get more specific.
Using the Analysis Tool
Back to the Melanoma example…

Using the Analysis Tool

Using the Analysis Tool

Using the Analysis Tool

Using the Analysis Tool

Practice 7.2 Question 1
Which of the following hypotheses is the overall test using in the Melanoma example?
- \(H_0: \beta_{\text{Lat}} = \beta_{\text{Ocean}} = \beta_{\text{Long}}\); \(H_a: \text{At least one $\beta$ is different from the others}\)
- \(H_0: \beta_{\text{Lat}} = \beta_{\text{Ocean}} = \beta_{\text{Long}}\); \(H_a: \beta_{\text{Lat}} \neq \beta_{\text{Ocean}} \neq \beta_{\text{Long}}\)
- \(H_0: \beta_{\text{Lat}} = \beta_{\text{Ocean}} = \beta_{\text{Long}} = 0\); \(H_a: \text{At least one $\beta$ is different from 0}\)
- \(H_0: \hat{\beta}_{\text{Lat}} = \hat{\beta}_{\text{Ocean}} = \hat{\beta}_{\text{Long}} = 0\); \(H_a: \text{At least one $\hat{\beta}$ is different from 0}\)
Practice 7.2 Question 1 Answer
Which of the following hypotheses is the overall test using in the Melanoma example?
- \(H_0: \beta_{\text{Lat}} = \beta_{\text{Ocean}} = \beta_{\text{Long}}\); \(H_a: \text{At least one $\beta$ is different from the others}\)
- \(H_0: \beta_{\text{Lat}} = \beta_{\text{Ocean}} = \beta_{\text{Long}}\); \(H_a: \beta_{\text{Lat}} \neq \beta_{\text{Ocean}} \neq \beta_{\text{Long}}\)
- \(H_0: \beta_{\text{Lat}} = \beta_{\text{Ocean}} = \beta_{\text{Long}} = 0\); \(H_a: \text{At least one $\beta$ is different from 0}\)
- \(H_0: \hat{\beta}_{\text{Lat}} = \hat{\beta}_{\text{Ocean}} = \hat{\beta}_{\text{Long}} = 0\); \(H_a: \text{At least one $\hat{\beta}$ is different from 0}\)
Practice 7.2 Question 2
What is the appropriate conclusion of the overall test of regression in the Melanoma example? Use \(\alpha = 0.01\).
- Reject the null hypothesis and conclude that at least 1 explanatory variables significantly explains mortality.
- Fail to reject the null hypothesis and conclude that at least 1 explanatory variables significantly explains mortality.
- Reject the null hypothesis and conclude that none of the explanatory variables significantly explains mortality.
- Fail to reject the null hypothesis and conclude that none of the explanatory variables significantly explains mortality.
- This test should not be done because the LINE assumptions do not hold for this analysis.
Practice 7.2 Question 2 Answer
What is the appropriate conclusion of the overall test of regression in the Melanoma example? Use \(\alpha = 0.01\).
- Reject the null hypothesis and conclude that at least 1 explanatory variables significantly explains mortality.
- Fail to reject the null hypothesis and conclude that at least 1 explanatory variables significantly explains mortality.
- Reject the null hypothesis and conclude that none of the explanatory variables significantly explains mortality.
- Fail to reject the null hypothesis and conclude that none of the explanatory variables significantly explains mortality.
- This test should not be done because the LINE assumptions do not hold for this analysis.
Research Objective
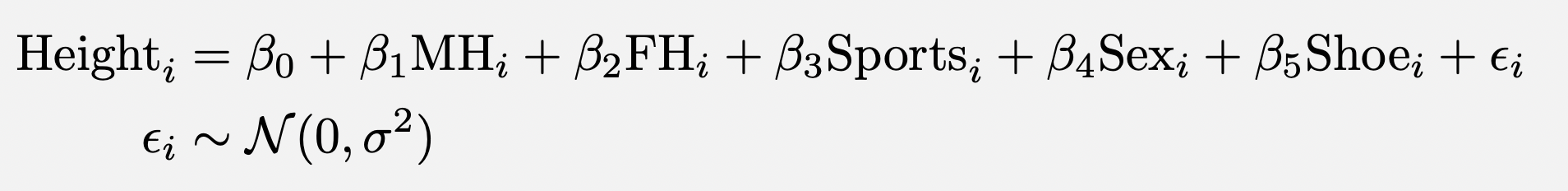
Research Question: Is the height of a student influenced by whether they played sports in HS?
What would it mean if \(\beta_3 = 0\)?
- There is no relationship between the height (y) and sports in HS (x).
Population vs. Sample Slope
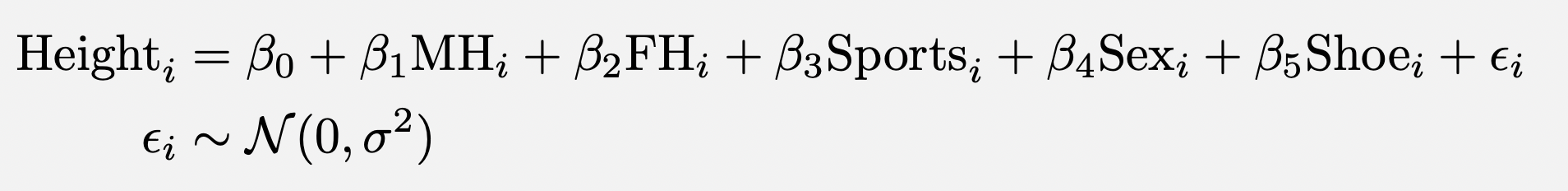
Our fitted model: \[\hat{y} = 23.26 + 0.28 \times \text{MH}_i + 0.21 \times \text{FH}_i + 0.35\times \text{Sports}_i + 3.19\times \text{Sex}_i + 1.06\times \text{Shoe}_i \]
So, doesn’t this mean that \(\beta_3 \neq 0\) because \(\hat{\beta}_3 = 0.348\)?
- Not necessarily! \(\beta_3 \neq \hat{\beta}_3\)
- We need to do a test for \(\beta_3\)
Hypothesis Testing for a Single slope
Research Question: Does sports in HS impact height?
Steps of hypothesis testing:
- Formulate null and alternative hypotheses.
- Gather the data and see if our sample data matches (or doesn’t match) the null hypothesis.
- Draw a conclusion about \(H_0\).
Hypothesis Testing for a Single slope
Knowing what we did with other hypothesis tests, how would we write out our hypotheses? \[ \begin{align} H_0: & \\ H_a: & \end{align} \]
Hypothesis Testing for a Single slope
Knowing what we did with other hypothesis tests, how would we write out our hypotheses? \[ \begin{align} H_0: & \beta_3 = 0 \\ H_a: & \beta_3 \neq 0 \\ \end{align} \]
Hypothesis Testing for a Single Slope
Step 2 - - gather the data and see if our sample data matches (or doesn’t match) the null hypothesis (note: do this only if LINE assumptions are valid)
Measuring if our data is consistent with the null hypothesis:
- Standardized test statistic: the number of standard errors away from the hypothesized value our data is. In our height example \(t =\) 3.2148829.
- \(p\)-value: probability of observing our sample result or “more extreme” (as stated by \(H_a\)) if the null hypothesis is true. Our \(p\)-value is 0.001.
Step 3: Draw a conclusions about \(H_0: \beta_3=0\). Using \(\alpha = 0.05\), what do we conclude about \(\beta_3\)?
- Our data is NOT consistent with the null hypothesis so we conclude that the sports in HS does have an effect on height.
Vagueness of Hypothesis Tests
If we reject \(H_0: \beta_3 = 0\) and conclude \(H_A: \beta_3 \neq 0\) then we really haven’t concluded anything other than there is an effect.
CIs for a Single Slope
Research Question: Comparing individuals who played sports in HS to those who didn’t, what is the difference in height?
Answer:
- A 95% confidence interval for \(\beta_3\) is calculated as (0.136,0.561).
- How do we interpret this interval?
- Holding all else constant, we are 95% confident that if a student played sports in HS vs not, we expect their height to be between 0.136 and 0.561 inches taller.
- Notice, that the interpretation says expect NOT will.
Using the Analysis Tool

Practice 7.2 Question 3
Using individual tests, which of the following significantly explain mortality? Mark all that apply.
- Latitude
- Longitude
- Ocean
Practice 7.2 Question 3 Answer
Using individual tests, which of the following significantly explain mortality? Mark all that apply.
- Latitude
- Longitude
- Ocean
Nuances of MLR Inference
Reminder that correlation is not causation:
- Just because you found a significant effect, does not mean that the explanatory variable causes and change in the response.
- Causation is established with experimentation
Nuances of MLR Inference
Directionality: MLR just exploits correlation even if the direction doesn’t make sense. Does X lead to a change in Y or does Y lead to a change in X?
- Does father’s height lead to an increase in child’s height or vice versa?
- Does sports in high school lead to an increase in child’s height or vice versa?
Nuances of MLR Inference
What do we do if the LINE assumptions aren’t quite appropriate?
- Throw out outliers (not recommended)
- Ignore them and do inference anyway (but acknowledge that your inferences could be very wrong - not recommended)
- Use more explanatory variables (we left a lot out).
- Consult a statistician (or better yet - take more stats classes and we’ll teach you)
Practice 7.2 Question 4
True or false: Based on our analysis, being in an oceanside state causes increases in mortality.
- True
- False
Practice 7.2 Question 4 Answer
True or false: Based on our analysis, being in an oceanside state causes increases in mortality.
- True
- False
Additional MLR Inference Practice:
Measuring possum head size can be difficult. However, other characteristics of the possum which are easier to measure may be associated with head size. Use sex, age, total length and tail length as explanatory variables to explain head size and answer the following questions.
- Do the LINE assumptions hold for the possum dataset?
- Yes
- Do any of sex, age, total length or tail length have an effect on head length? Use \(\alpha = 0.05\).
- Yes - the F statistic is 29.461 with a p-value of 0.
Additional MLR Inference Practice:
Measuring possum head size can be difficult. However, other characteristics of the possum which are easier to measure may be associated with head size. Use sex, age, total length and tail length as explanatory variables to explain head size and answer the following questions.
- Which of sex, age, total length and tail length have an effect on head length? Use \(\alpha = 0.05\).
- All of them except tail length.
- If the total length goes up by 1, how much do we expect the head length to change? Use 90% confidence level.
- Estimate of 0.6381 with a 90% interval of (0.5184, 0.7579).
Key Terminology
- LINE Assumptions
- Overall Hypothesis tests
- Hypothesis tests for single slope
- Confidence intervals for \(\beta_1\)
- Checking LINE assumptions