Simple Linear Regression - Inference

Research Objective

Research Question: Is the adult height of a student determined by the height of the mother? In other words, what is the relationship between a student’s height and mother’s height for all BYU students?

Population: All BYU students.

Parameter of Interest:

The slope between mother’s height and student’s height.

Sample: A convenience sample of 1727 BYU students who are in Stat 121.

Are there any issues with this study setup?

Research Objective

Our model: \(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\).

Considering the research question, What would it mean if \(\beta_1 = 0\)?

There is no relationship between mother’s height (x) and student’s height (y).

Population vs. Sample Slope

Our model: \(y_i = \beta_0 + \beta_1x_i + \epsilon_i\)

Our fitted model: \(\hat{y} = 35.653 + 0.503\times x\)

So, doesn’t this mean that \(\beta_1 \neq 0\) because \(\hat{\beta}_1 = 0.503\)?

Not necessarily! \(\beta_1 \neq \hat{\beta}_1\)
We need to do a test for \(\beta_1\)

Hypothesis Testing for \(\beta_1\)

Research Question: Does mother’s height impact a child’s height?

Steps of hypothesis testing:

Formulate null and alternative hypotheses.
Gather the data and see if our sample data matches (or doesn’t match) the null hypothesis.
Draw a conclusion about \(H_0\).

Practice 6.3 Question 1

Knowing what we did with other hypothesis tests, select the correct hypotheses \[ \begin{align} H_0: & \\ H_a: & \end{align} \]

\(H_0: \hat{\beta}_1 = 0; H_A: \hat{\beta}_1 \neq 0\)
\(H_0: \beta_1 = 0; H_A: \beta_1 \neq 0\)
\(H_0: \mu = 0; H_A: \mu \neq 0\)
\(H_0: \pi = 0; H_A: \pi \neq 0\)

Practice 6.3 Question 1 Answer

Knowing what we did with other hypothesis tests, select the correct hypotheses \[ \begin{align} H_0: & \\ H_a: & \end{align} \]

\(H_0: \hat{\beta}_1 = 0; H_A: \hat{\beta}_1 \neq 0\)
\(H_0: \beta_1 = 0; H_A: \beta_1 \neq 0\)
\(H_0: \mu = 0; H_A: \mu \neq 0\)
\(H_0: \pi = 0; H_A: \pi \neq 0\)

Hypothesis Testing for \(\beta_1\) - Step 2

Step 2 - Compare our data result with what we expect to see if the null hypothesis is true.

From our sample, we have \(\hat{\beta}_1 = 0.503\) is this “different enough” from \(0\) to conclude that \(H_a: \beta_1 \neq 0\)?

Hypothesis Testing for \(\beta_1\) - Step 2

Step 2 - Compare our data result with what we expect to see if the null hypothesis is true.

From our sample, we have \(\hat{\beta}_1 = 0.503\) is this “different enough” from \(0\) to conclude that \(H_a: \beta_1 \neq 0\)?

First, standardize using the formula (or let the computer do this for you): \[ t = \frac{\hat{\beta}_1 - \overbrace{\beta_1}^{0}}{\frac{\hat{\sigma}}{\sum_{i=1}^n (x_i-\bar{x})^2}} = 15.914 \] Interpret \(t\) as the number of standard errors our \(\hat{\beta}_1\) is from the hypothesized \(\beta_1\).

Practice 6.3 Question 2

Is \(t = 15.914\) “different enough” from the null hypothesis to make us think the null is wrong?

What statistical tool do we use to assess this question?

Central Limit Theorem
Sampling Distribution of \(t\)
Independence
Law of Large Numbers

Practice 6.3 Question 2 Answer

Is \(t = 15.914\) “different enough” from the null hypothesis to make us think the null is wrong?

What statistical tool do we use to assess this question?

Central Limit Theorem
Sampling Distribution of \(t\)
Independence
Law of Large Numbers

Hypothesis Testing for \(\beta_1\) - Step 2

If the LINE assumptions of the regression model are appropriate, then \[ t = \frac{\hat{\beta}_1 - \overbrace{\beta_1}^{0}}{\frac{\hat{\sigma}}{\sum_{i=1}^n (x_i-\bar{x})^2}} \] is a standardized statistic and follows \(t\) distribution with center \(0\) and spread \(1\) and degrees of freedom \(n-2\).

Note, above we would set \(\beta_1 = 0\) because we assume \(H_0\) is true unless proven otherwise.

So…what does this mean?

Hypothesis Testing for \(\beta_1\) - Step 2

IF the LINE assumptions holds, the talues of \(t\) that are consistent with the claim \(H_0: \beta_1 = 0\) are given by the distribution (curve):

But we are getting ahead of ourselves because the LINE assumptions have to be true for the above picture to be correct.

Checking LINE Assumptions

Reminder, the LINE assumptions are:

L - Linear relationship between \(x\) and \(y\)
I - Independence (one obs. doesn’t impact the other)
N - Normal residuals (distance from line is normal)
E - Equal variance of residuals (spread about the line is constant)

How would we see if there is a linear relationship between \(x\) and \(y\)?

Scatterplot!

Checking LINE Assumptions

Is this (approximately) linear for the bulk of the data?

Checking LINE Assumptions

How would we see if there is independence? In other words, how can we “check” if one observation doesn’t influence another?

Critical Thinking!

Does it make sense that one student’s height would determine another student’s height?

Likely a minimal influence.

Checking LINE Assumptions

How would we see if the residuals are normal?

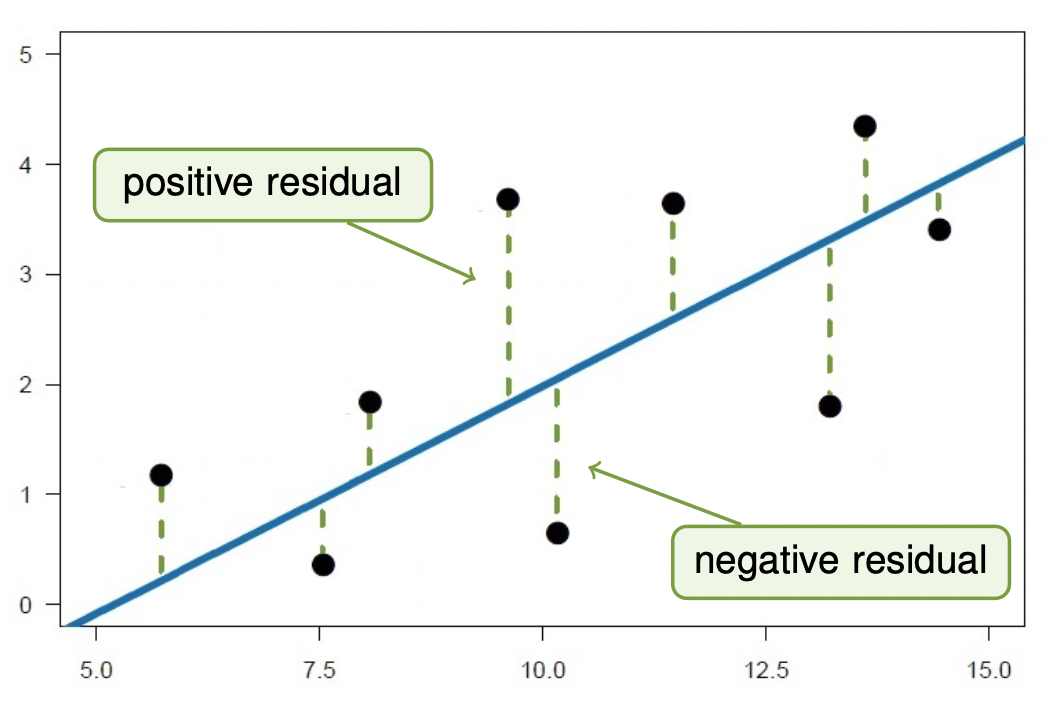
Calculate the residuals as \(\epsilon_i = y_i - (\hat{\beta}_0 + \hat{\beta}_1x_i)\) (don’t worry - the computer will do this for you)
Draw a histogram (or density plot) of residuals

Checking LINE Assumptions

How would we see if the residuals are normal?

Calculate the residuals as \(\epsilon_i = y_i - (\hat{\beta}_0 + \hat{\beta}_1x_i)\) (don’t worry - the computer will do this for you)
Draw a histogram (or density plot) of residuals

Is this approximately normal?

Close enough. Skew = 0.0526991

Checking LINE Assumptions

How would we see if there is “equal spread” of the residuals about the fitted line?

Checking LINE Assumptions

How would we see if there is “equal spread” of the residuals about the fitted line?

Option 1: Scatterplot with fitted line

Checking LINE Assumptions

How would we see if there is “equal spread” of the residuals about the fitted line?

Option 2: Fitted values vs. residuals plot (just like a scatterplot with fitted line but made to be easier to see visually)

Is this roughly “equal spread”?

Close enough except for 1 or 2 outliers

Checking LINE Assumptions

Examples of NOT equal spread

Using the Analysis Tool

Melanoma is highly related to sun exposure. Hence, areas with greater sun have a greater risk of melanoma.

Using the Analysis Tool

Practice 6.3 Question 3

Use the analysis tool to check the following assumptions for the Melanoma example. Which of the following assumptions hold (check all that apply):

Linearity
Independence
Normality of Residuals
Equal Spread of Residuals

Practice 6.3 Question 3 Answer

Use the analysis tool to check the following assumptions for the Melanoma example. Which of the following assumptions hold (check all that apply):

Linearity
Independence
Normality of Residuals
Equal Spread of Residuals

Hypothesis Testing for \(\beta_1\)

Back to Step 2 - - gather the data and see if our sample data matches (or doesn’t match) the null hypothesis (note: do this only if LINE assumptions are valid)

Measuring if our data is consistent with the null hypothesis:

Standardized test statistic: the number of standard errors away from the hypothesized value our data is. In our rent example \(t =\) 15.9137202.
\(p\)-value: probability of observing our sample result or “more extreme” (as stated by \(H_a\)) if the null hypothesis is true. Our \(p\)-value is 0.

Step 3: Draw a conclusions about \(H_0: \beta_1=0\). Using \(\alpha = 0.05\), what do we conclude about \(\beta_1\)?

Our data is NOT consistent with the null hypothesis so we conclude that the mother’s height does have an effect on the student’s height.

Using the Analysis Tool

Vagueness of Hypothesis Tests

If we reject \(H_0: \beta_1 = 0\) and conclude \(H_A: \beta_1 \neq 0\) then we really haven’t concluded anything other than there is an effect.

Use a confidence interval for more informative answers.

Confidence Intervals for \(\beta_1\)

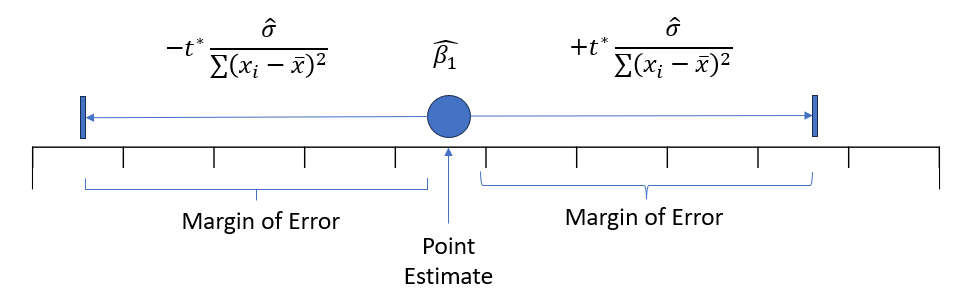
Using the same ideas for building a confidence interval as before, a C% confidence interval for \(\beta_1\) is: \[ \hat{\beta}_1 \pm t^\star\frac{\hat{\sigma}}{\sum_{i=1}^n (x_i-\bar{x})^2} \]

Don’t worry about the formula, the computer will calculate it for you.

Confidence Intervals for \(\beta_1\)

Research Question: As the mother’s height increases, what happens to the child’s height?

Answer:

A 95% confidence interval for \(\beta_1\) is calculated as (0.441,0.565).
How do we interpret this interval?
- We are 95% confident that as the mother’s height goes up by 1 inch, we expect the student’s height to go up between (0.441,0.565) inches.
- Notice, that the interpretation says expect NOT will.

Using CIs to do Tests

Research Question: If the mother’s height goes up by 1 inch, can we expect the student’s height to change by 1in?

Answer:

A 95% confidence interval for \(\beta_1\) is calculated as (0.441,0.565).

No because 1 is not in the interval at the 0.05 significance level.

Principle: You can use CIs to do 2-sided hypothesis tests (i.e. alternative hypothesis with “\(\neq\)”)

Using the Analysis Tool

Practice 6.3 Question 4

Suppose that someone wanted to use longitude instead of latitude to explain Melanoma mortality. Assuming all the LINE assumptions hold, can we conclude that longitude has a linear effect on melanoma mortality?

No because we reject the null hypothesis.
Yes because we reject the null hypothesis.
No because we fail to reject the null hypothesis.
Yes because we fail to reject the null hypothesis.

Practice 6.3 Question 4 Answer

No because we reject the null hypothesis.
Yes because we reject the null hypothesis.
No because we fail to reject the null hypothesis.
Yes because we fail to reject the null hypothesis.

Nuances of Inference for \(\beta_1\)

What do we do if the LINE assumptions aren’t quite appropriate?

Throw out outliers (not recommended)
Ignore them and do inference anyway (but acknowledge that your inferences could be very wrong - not recommended)
Use more explanatory variables. For example, use father’s height AND shoe size to explain height (we’ll learn this next unit).
Consult a statistician (or better yet - take more stats classes and we’ll teach you)

Additional Practice:

Measuring possum head size can be difficult. However, measuring total possum length is easier. What is the relationship between possum length and head size? Use a simple linear regression model (and the course app) to answer the following questions:

Do the LINE assumptions all hold for this example?
- Yes
Does total length have a linear effect on head length?
- Yes because the test on the slope rejects at the \(\alpha = 0.05\) level.
What would a Type 1 Error be for the hypothesis test in #1?
- Saying there is a relationship between total and head length when there isn’t.
If the total length goes up by 1, how much do we expect the head length to change?
- We are 90% confident that head length will go up between (0.6904, 0.977)

Key Terminology

LINE Assumptions
Hypothesis tests for \(\beta_1\)

Confidence intervals for \(\beta_1\)
Checking LINE assumptions