Simple Linear Regression - EDA
A Real Study
- Background: Disposing ash from burning coal (power plants) disposal in open fields is an environmental concern. One solution is to put ash into mortars and reuse it.
- Question: Can the amount of ash in mortars compromise the strength of the mortar?
- Conclusion: Significant positive relationship between ash and mechanical properties of mortars.
In this unit:
- How do we analyze the effect of a quantitative explanatory variable (amount of ash) on a quantitative response (strength of the mortar)?
Reminder
The process of statistical analysis:
- Identify research question and the corresponding population and parameter you are interested in.
- Collect data.
- Posit a statistical model based on information in the sample.
- Draw inference about the population using your model.
Research Objective
Research Question: Is the adult height of a child determined by the height of the mother? In other words, what is the relationship between student’s height and mother’s height for all BYU students”
Population: All BYU students.
Parameter of Interest:
- Some number measuring the “relationship” between students height and the mother’s height.
Sample: A convenience sample of 1727 BYU students who are in Stat 121.
Are there any issues with this study setup?
More Problem Definitions
Response Variable (y): The height of the student.
- This is a continuous quantitative variable meaning it can be any number (including decimals)
Explanatory Variable (x): The height of the mother.
- This is also continuous quantitative variable.
Exploratory Data Analysis (EDA)
Main goal: Investigate the relationship between student’s height and mother’s height.
Tool #1 - Scatterplots

Tool #1 - Scatterplots
Things to look for in a scatterplot:
- Form: linear, non-linear or nothing
- Direction: positive or negative
- Strength: amount of “scatter” about the trend-line
- Outliers (data points out by themselves)
Tool #1 - Scatterplots w/trend line

Form? Direction? Strength? Outliers?
Tool #1 - Scatterplot Practice
Ecology example: Is possum length related to head length?

Form? Direction? Strength? Outliers?
Tool #1 - Scatterplot Practice
Engineering example: Is speed related to stopping distance?

Form? Direction? Strength? Outliers?
Tool #1 - Scatterplot Practice
Environment example: How much pollution do cars produce?

Form? Direction? Strength? Outliers?
Practice 6.1 Question 1
What is the form of this scatterplot?
- Linear
- Non-linear
Practice 6.1 Question 1 Answer
What is the form of this scatterplot?
- Linear
- Non-linear
Practice 6.1 Question 2
What is the direction of this scatterplot?
- Positive
- Negative
- Flat
Practice 6.1 Question 2 Answer
What is the direction of this scatterplot?
- Positive
- Negative
- Flat
Practice 6.1 Question 3
What is the strength of this scatterplot?
- More Strong than Weak
- More Weak than Strong
Practice 6.1 Question 3 Answer
What is the strength of this scatterplot?
- More Strong than Weak
- More Weak than Strong
Tool #1 - Scatterplot Practice

Which graph has a stronger relationship?
- Trick question- they are the same data!
- We need a numeric (objective) measure of strength.
Tool #2 - Covariance

Covariance: a measure of the linear relationship between y and x (how much y changes as x changes), but with units that are difficult to interpret. \[ \begin{align} \text{Cov}(X,Y) &= \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \\ &= 4.159 \end{align} \]
Tool #2 - Covariance
Properties of Covariance:- If \(\text{Cov}(X,Y) < 0 \Rightarrow\) negative linear relationship
- If \(\text{Cov}(X,Y) > 0 \Rightarrow\) positive linear relationship
- Highly impacted by the unit of measurements for \(X\) and \(Y\).
- Highly impacted by outliers
- What we really want is a standardized measure of strength
Tool #3 - Correlation

Correlation: A standardized measure of strength between -1 and 1: \[ \begin{align} \text{Corr}(X,Y) = r &= \frac{1}{n-1}\sum_{i=1}^n \left(\frac{x_i - \bar{x}}{s_x}\right)\left(\frac{y_i - \bar{y}}{s_y}\right) \\ &= 0.358 \end{align} \]
Tool #3 - Correlation
Properties of Correlation (r):- \(-1 < r < 1\)

Tool #3 - Correlation
Properties of Correlation (r):- \(-1 < r < 1\)
- Only appropriate for LINEAR relationships

Tool #3 - Correlation
Properties of Correlation (r):- \(-1 < r < 1\)
- Only appropriate for LINEAR relationships
- NOT impacted by scale of data (scale invariant). For example: \[ \begin{align} \text{Cor}(\text{Height in inches, Weight in pounds}) = \\ \text{Cor}(\text{Height in meters, Weight in kg}) \end{align} \]
Tool #3 - Correlation
Properties of Correlation (r):- \(-1 < r < 1\)
- Only appropriate for LINEAR relationships
- NOT impacted by scale of data (scale invariant). For example:
- Highly impacted by outliers
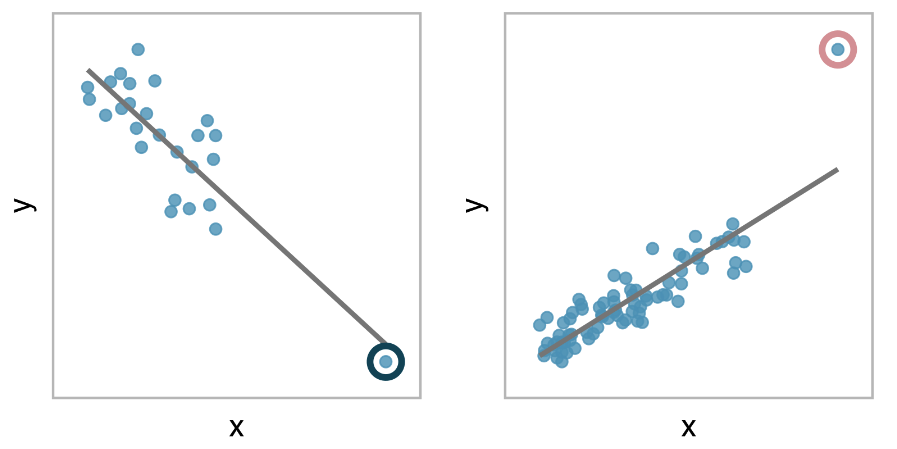
In one case the outlier made \(r\) go up, in the other \(r\) goes down.
Tool #3 - Correlation
Properties of Correlation (r):- \(-1 < r < 1\)
- Only appropriate for LINEAR relationships
- NOT impacted by scale of data (scale invariant). For example:
- Highly impacted by outliers
- Only for 2 quantitative variables. For example, correlation between state and income doesn’t make sense.
Tool #3 - Correlation
Properties of Correlation (r):- \(-1 < r < 1\)
- Only appropriate for LINEAR relationships
- NOT impacted by scale of data (scale invariant). For example:
- Highly impacted by outliers
- Only for 2 quantitative variables. For example, correlation between state and income doesn’t make sense.
- \(\text{Cor}(X,Y) = \text{Cor}(Y,X)\)
Practice 6.1 Question 4
True or False: If \(r=0\) there is no relationship between the explanatory and response variables.
- True
- False
Practice 6.1 Question 4 Answer
True or False: If \(r=0\) there is no relationship between the explanatory and response variables.
- True
- False - \(r=0\) only means there is no linear relationship but there could be a non-linear relationship so make sure you plot the data first
Using the Analysis Tool

Using the Analysis Tool

Using the Analysis Tool

Correlation is not causation
Just because two variables are correlated, does not mean that one causes the other. For example (examples taken from spurious correlations):
The correlation between the number of movies made by Nicolas Cage and the number of drowning deaths is 0.66. Does this mean that Nicolas Cage movies cause drownings?
The correlation between the number of global shark attacks and ice cream sales in 0.81. Does this mean that shark attacks cause people to buy ice cream?
The correlation between the per capita consumption of margarine and the divorce rate in Maine is 0.99. Does this mean that eating more margarine causes divorce?
Homework Choices for Unit 6
- Rate my professor - what matters in determining a rate my professor score?
- Supervisor - what makes people like their manager?
- Body Fat - what body measurements are predictive of your BMI?
- Basketball Salary - what skills lead to a higher salary?
Key Terminology
- Scatterplot
- Form
- Direction
- Strength
- Outliers
- Correlation and Properties
- Covariance and Properties
