| College | n | Mean | SD | Min | Q1 | M | Q3 | Max | Skew |
|---|---|---|---|---|---|---|---|---|---|
| Business | 608 | 13.93 | 8.97 | 0 | 7 | 12 | 20 | 50 | 1.08 |
| CMS | 177 | 15.21 | 9.46 | 2 | 8 | 14 | 20 | 50 | 1.00 |
Comparing 2 Means
A Real Analysis
- Background: Disasters are expensive for everyone
- Data: Economic Loss data and various factors caused by natural disasters were collected
- Conclusion: Research found that disaster type, season, and area have significant influence on direct economic loss and affected population
In this unit:
- How can we analyze the impact of a categorical explanatory variable (disaster type) on a numeric (quantitative) response (economic loss)?
Reminder
The process of statistical analysis:
- Identify population and parameter you are interested in.
- Collect data
- Posit a statistical model based on information in the sample
- Draw inference about the population using your model
Research Objective
Research Question: Is the average number of hours of homework done per week done by students in Business less than the number of hours of homework per week in CMS?
Population: All BYU students in Business or CMS.
Parameter of Interest:
- We actually have two: \(\mu_1\) is the mean number of hours of homework in Business and \(\mu_2\) is the mean number of hours of homework in CMS.
Sample: A convenience sample of 785 BYU students who are in 121 and completed the student survey AND who are either in Business or CMS.
Are there any issues with this study setup?
More Problem Definitions
Response Variable (y): The average number of hours of homework per week.
- This is a continuous quantitative variable meaning it can be any number (including decimals)
Explanatory Variable (x): The college (either Business or CMS).
Exploratory Data Analysis (EDA)
Main goal: Compare the distribution of hours of homework in Business and CMS.
EDA Tool #1 - Histograms

EDA Tool #1 - Histograms

EDA Tool #2 - Density Plots

How would you describe shape, center, and spread?
EDA Tool #3 - Boxplots

EDA Tool #4 - Numerical Summaries
Example: Website Design
An “A/B test” is a experiment with a two factor explanatory variable (two groups) and is commonly used to see which of two treatments is superior. In one such A/B test a company was testing two different website designs for selling their product. Visitors to the website were randomly assigned to one of two designs and the visitors were monitored for how much they spent on the site. Researchers want to know if there is a difference in revenue between the two website designs. The results are given in the “Website Designs” dataset on the course analysis website.
Using the Tool for EDAs

Using the Tool for EDAs

Using the Tool for EDAs

Statistical Model

Statistical Model
Important notes about the model:
- Because we want to compare, we are primarily interested in \(\mu_1 - \mu_2\).
- Skewness of both groups should be “close” to zero (remeber rule of thumb is between -0.5 and 0.5).
-
There is a common standard deviation (\(\sigma\)) between the two groups.
- A good rule of thumb to check if this assumption is valid is that the \(\max(s_1, s_2)/\min(s_1, s_2) < 2\).
Practice 4.1 Question 1
For the website design analysis, does the two means population model apply?
- Yes because revenue for both groups are roughly normal and have approximately equal standard deviations.
- Yes because the revenue in the “A” group is roughly normal.
- No because revenue in at least one group is skewed.
- No because the standard deviations of revenue in each group are not approximately equal.
Practice 4.1 Question 1 Answer
For the website design analysis, does the two means population model apply?
- Yes because revenue for both groups are roughly normal and have approximately equal standard deviations.
- Yes because the revenue in the “A” group is roughly normal.
- No because revenue in at least one group is skewed.
- No because the standard deviations of revenue in each group are not approximately equal.
Point Estimation
The parameters we want to estimate are
- \(\mu_1 - \mu_2\)
- \(\sigma\)
so we use
- \((\bar{y}_1 - \bar{y}_2) \rightarrow \mu_1-\mu_2\)
- \(s = \sqrt{\frac{\sum_{i=1}^{n_1}(y_i - \bar{y}_1)^2 + \sum_{i=1}^{n_2}(y_i - \bar{y}_2)^2}{n_1+n_2-2}} \rightarrow \sigma\)
Point Estimation
How good of an estimate is \(\bar{y}_1-\bar{y}_2\) to \(\mu_1-\mu_2\)?
As the sample sizes (\(n_1\) and \(n_2\)) get bigger, the probability that \(\bar{y}_1-\bar{y}_2\) gets closer and closer to \(\mu_1-\mu_2\) increases.
- Important note: how close \(\bar{y}_1-\bar{y}_2\) is to \(\mu_1-\mu_2\) depends on the smaller sample size. If one sample size is really small then \(\bar{y}_1-\bar{y}_2\) might be far away from \(\mu_1-\mu_2\) even if the other sample size is big.
Hypothesis Testing
Recall the 3 steps of hypothesis testing:
- Formulate hypotheses
- See if data matches (or doesn’t) match the hypotheses
- Draw conclusions about the parameter
Hypothesis Testing
Research Question: Is the average number of hours of homework per week done by students in Business less than the number of hours of homework per week in CMS?
How would you write the hypotheses? \[ \begin{align} H_0: & \\ H_a: & \\ \end{align} \]
Hypothesis Testing
Research Question: Is the average number of hours of homework per week done by students in Business (group “1”) less than the number of hours of homework per week in CMS (group “2”)?
Two ways to write the hypotheses: \[ \begin{align} H_0: & \mu_1 = \mu_2 \\ H_a: & \mu_1 < \mu_2 \end{align} \]
\[ \begin{align} H_0: & \mu_1 - \mu_2 = 0 \\ H_a: & \mu_1 - \mu_2 < 0 \end{align} \]
Practice 4.1 Question 2
In an A/B test a company was testing two different website designs for selling their product. Visitors to the website were randomly assigned to one of two designs and the visitors were monitored for how much they spent on the site. Researchers want to know if there is a difference in revenue between the two website designs. The results are given in the “Website Designs” dataset on the course analysis website.
What would be the null and alternative hypotheses in this scenario?- \(H_0: \mu_A = \mu_B\); \(H_A: \mu_A > \mu_B\)
- \(H_0: \mu_A = \mu_B\); \(H_A: \mu_A < \mu_B\)
- \(H_0: \mu_A = \mu_B\); \(H_A: \mu_A \neq \mu_B\)
- \(H_0: \pi_A = \pi_B\); \(H_A: \pi_A > \pi_B\)
- \(H_0: \pi_A = \pi_B\); \(H_A: \pi_A < \pi_B\)
- \(H_0: \pi_A = \pi_B\); \(H_A: \pi_A \neq \pi_B\)
Practice 4.1 Question 2 Answer
In an A/B test a company was testing two different website designs for selling their product. Visitors to the website were randomly assigned to one of two designs and the visitors were monitored for how much they spent on the site. Researchers want to know if there is a difference in revenue between the two website designs. The results are given in the “Website Designs” dataset on the course analysis website.
What would be the null and alternative hypotheses in this scenario?- \(H_0: \mu_A = \mu_B\); \(H_A: \mu_A > \mu_B\)
- \(H_0: \mu_A = \mu_B\); \(H_A: \mu_A < \mu_B\)
- \(H_0: \mu_A = \mu_B\); \(H_A: \mu_A \neq \mu_B\)
- \(H_0: \pi_A = \pi_B\); \(H_A: \pi_A > \pi_B\)
- \(H_0: \pi_A = \pi_B\); \(H_A: \pi_A < \pi_B\)
- \(H_0: \pi_A = \pi_B\); \(H_A: \pi_A \neq \pi_B\)
Hypothesis Testing
Step 2: See if the data matches the hypotheses.
- We need (1) a measure of how different what we observed in our sample is from what we expect to have observed if the null hypothesis is true and (2) if our observed difference is “big enough” to reject \(H_0\).
Hypothesis Testing - Step 2
As before, we want to use standardized differences between \(\bar{y}_1-\bar{y}_2\) and \(\mu_1-\mu_2 = 0\) (by hypothesis) but, because we have two means, the formula changes to: \[ t = \frac{(\bar{y}_1-\bar{y}_2) - (\mu_1 - \mu_2)}{s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} = -1.648\]
- Don’t worry about the formula (we’ll use the tool to calculate it for us)
- How do we interpret this standardized value?
- Our sample difference of \(\bar{y}_1 - \bar{y}_2\) = -1.279 (recall “business” = “group 1”) is -1.648 standard errors away from the hypothesized difference of \(\mu_1 - \mu_2 = 0\).
Hypothesis Testing - Step 2
So, is a \(t\) of -1.648 “different enough” for us to reject \(H_0\)?
- That depends on the sampling distribution of \(t\)!
- Reminder: The sampling distribution of \(t\) tells us the values that \(t\) can be when sampling from “two means model” population IF the null hypothesis is true.
Hypothesis Testing
If the “two means model” from before is appropriate and the null hypothesis \(H_0: \mu_1 = \mu_2\) is true, then \[ t = \frac{\bar{y}_1-\bar{y}_2 - (\mu_1 - \mu_2)}{s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \] is a standardized test statistic for the null hypothesis and follows a t-distribution with mean \(0\) and spread \(1\) and degrees of freedom \(n_1+n_2-2\).
Important: check if the two means model is appropriate by (1) histogram of each group and (2) see if the standard deviations are “close enough” to equal via \(\max(s_1,s_2)/\min(s_1, s_2) < 2\).
- So…what does this mean?
Hypothesis Testing
If the population two means models, then \(t\) should fall within this curve IF the null hypothesis is true:
\(t =\) -1.648
Hypothesis Testing
Step 2: See if the data matches the hypotheses.

\(t =\) -1.648
\(p\)-value \(=\) 0.0498584
Hypothesis Testing
Step 3: Draw a conclusion (use \(\alpha = 0.05\))
Given that:
- \(t =\) -1.648
- \(p\)-value \(=\) 0.05
What should we conclude?
- Our data are inconsistent with the null hypothesis so we reject the null and conclude that the mean number of hours of homework by students in Business is less than the mean number of hours of homework by students in CMS.
Using the Tool

Practice 4.1 Question 3
For the website design analysis, what is the appropriate conclusion of the hypothesis test (use \(\alpha = 0.05\))?- Reject \(H_0\) and conclude that the website designs have the same revenue.
- Reject \(H_0\) and conclude that the website designs have different revenue.
- Fail to reject \(H_0\) and conclude that the website designs have the same revenue.
- Fail to reject \(H_0\) and conclude that the website designs have different revenue.
Practice 4.1 Question 3 Answer
For the website design analysis, what is the appropriate conclusion of the hypothesis test (use \(\alpha = 0.05\))?- Reject \(H_0\) and conclude that the website designs have the same revenue.
- Reject \(H_0\) and conclude that the website designs have different revenue.
- Fail to reject \(H_0\) and conclude that the website designs have the same revenue.
- Fail to reject \(H_0\) and conclude that the website designs have different revenue.
Confidence Intervals
Hypothesis test conclusions can be vague so lets build a confidence interval. To build a confidence interval for \(\mu_1-\mu_2\), we know from the previous theorem that \(C\%\) of the time,
\[ \begin{align} - t^\star < \frac{\bar{y}_1-\bar{y}_2 - (\mu_1 - \mu_2)}{s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} < t^\star \end{align} \]

Confidence Intervals
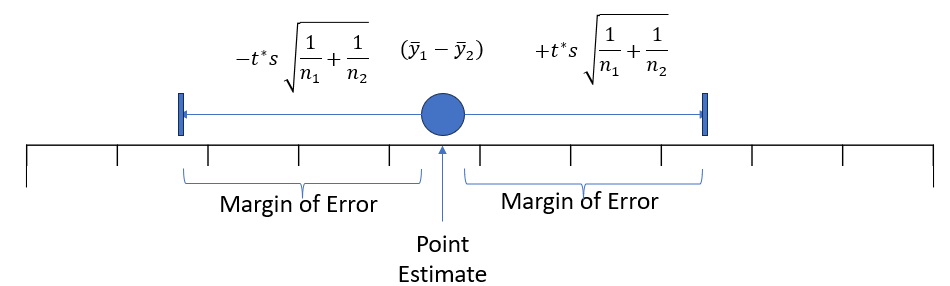
A C% confidence interval for \(\mu_1-\mu_2\) is given by:
\[ \begin{align} (\bar{y}_1-\bar{y}_2) \pm t^\star s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}} \end{align} \]
Confidence Intervals
A 95% confidence interval for \(\mu_1-\mu_2\) is (-2.802, 0.244). How do we interpret this interval?
- We are 95% confident that the difference in the mean number of hours spent on HW for all students in Business minus the mean number of hours spent on HW for all students in CMS is between -2.802 and 0.244.
Using the Tool

Using the Tool

Practice 4.1 Question 4
How do we interpret a 90% interval in the website design analysis?- We are 90% sure that the difference between the mean revenue for design A minus the mean revenue for design B is between -5.2165 and -4.1523.
- We are 90% confident that the difference between the mean revenue for design A minus the mean revenue for design B is between -5.3184 and -4.0504.
- We are 90% confident that the difference between the sample mean revenue for design A minus the sample mean revenue for design B is between -5.2165 and -4.1523.
- We are 90% confident that the difference between the mean revenue for design A minus the mean revenue for design B is between -5.2165 and -4.1523.
Practice 4.1 Question 4 Answer
How do we interpret a 90% interval in the website design analysis?- We are 90% sure that the difference between the mean revenue for design A minus the mean revenue for design B is between -5.2165 and -4.1523.
- We are 90% confident that the difference between the mean revenue for design A minus the mean revenue for design B is between -5.3184 and -4.0504.
- We are 90% confident that the difference between the sample mean revenue for design A minus the sample mean revenue for design B is between -5.2165 and -4.1523.
- We are 90% confident that the difference between the mean revenue for design A minus the mean revenue for design B is between -5.2165 and -4.1523.
Nuances of Inference
- In order to do inference (a hypothesis test or a confidence interval), the two means models needs to apply. What do we do if the histograms (density plots) aren’t normal? Remember that our model assumes that our data come from a normal population with different means.
Nuances of Inference
- In order to do inference (a hypothesis test or a confidence interval), the two means models needs to apply. What do we do if the histograms (density plots) aren’t normal? Remember that our model assumes that our data come from a normal population with different means.
If the normal model is not appropriate BUT you have large sample sizes, the distribution of \(t\) is still approximately a \(t\)-distribution with center \(0\), spread \(1\) and degrees of freedom \(n_1+n_2-2\).
For this class, we will use \(n_1>30\) and \(n_2>30\) as “large.”
Nuances of Inference
- In order to do inference (a hypothesis test or a confidence interval), the two means models needs to apply. What do we do if the standard deviations aren’t equal?
- Consult a statistician but you would be surprised how often equal standard deviations is actually close enough to true.
- The consequence is that the CLT allows us to do inference if the population is not normal but we can’t do inference if the standard deviations are not approximately equal.
Nuances of Inference
-
Keep in mind key terms of hypothesis tests:
-
What would constitute Type 1 and Type 2 errors for our hours of homework analysis?
- Type 1 = concluding Business spends less time on HW than CMS when, in, fact they spend the same time.
- Type 2 = concluding Business spends the same time on HW as CMS when, in, fact they spend less time.
-
Are our results “statistically significant”?
- Yes because we rejected H0
-
Are our results “practically significant”?
- Maybe (which way would you argue?)
-
How would we increase the power of our test?
- We could increase sample size or increase \(\alpha\).
-
Nuances of Inference
-
Keep in mind key terms of confidence intervals:
-
Margin of error
- Interval = Point Estimate \(\pm\) Margin of Error
-
Effect of sample size on margin of error
- As sample sizes go up, margin of error goes down.
-
Effect of confidence level on margin of error
- As confidence level goes up, margin of error goes up.
-
HW This Unit
- Inmate stress - does putting inmates in isolation affect their mental health?
- Going to college - are there differences in grades based on peoples interest in college?
- Happiness - do different regions of the world have different happiness levels?
- NBA scoring - do different positions in basketball score more points per game?
Key Terminology
- A/B Testing
- Sampling distribution of \(\bar{y}_1-\bar{y}_2\)
- t-distribution
- Two means model
- Exploratory data analysis for two groups
- Interpreting a confidence interval
- Two-sample t-test
- Equal standard deviation between groups
