Confidence Intervals for Univariate Quantitative Data

Reminder

The process of statistical analysis:

  1. Identify population and parameter you are interested in.
    • Question: What is the average age at which BYU students find out Santa Claus isn’t real? Specifically, is the average age at which BYU students find out Santa isn’t real older than 8?
    • Parameter: The mean age at which all BYU students find out Santa Claus isn’t real. We’ll use the Greek letter \(\mu\) to denote this value.
  2. Collect data
    • A convenience sample of 1727 BYU students who are taking this course and completed the student survey.
  3. Posit a statistical model based on information in the sample
    • Explore the data.
    • Posited a normal population model.
  4. Draw inference about the population using your model.

Types of Statistical Inference

3 ways of using sample to make inference about the population:

  1. Point Estimation (last lecture notes)
  2. Hypothesis Testing (last lecture notes)
  3. Confidence Intervals

An Issue with Hypothesis Testing

A student claims that the average age BYU students learn about Santa Claus is 8. I hypothesize that its older than that. Perform a hypothesis test for these claims.

Step 3 - Draw a conclusion

  • Because the \(p\)-value is small. We say that our data is NOT consistent with the null hypothesis and that the mean is greater than 8.
  • “Conclusions” from hypothesis tests are painfully vague!
  • On the one hand, if we reject \(H_0\), we still don’t have a firm conclusion on what the value of the parameter is.
  • On the other hand, if we don’t reject \(H_0\), we can’t say \(H_0\) is true because we assumed it was true.

Confidence Intervals

Goal: Provide a range of reasonable values that the parameter could be.

Tool: The sampling distribution of \(t\).

Constructing a Confidence Intervals

If the normal population model is appropriate and the null hypothesis \(H_0: \mu = \mu_0\) is true, then \[ t = \frac{\bar{y} - \mu}{s/\sqrt{n}} \] is a standardized statistic and its sampling distribution is a \(t\)-distribution with center \(0\), spread \(1\) and degrees of freedom \(n-1\) where \(n\) is the size of the sample.

Constructing Confidence Intervals

According to the \(t\)-distribution:
  • 50% of possible \(t = (\bar{y}-\mu)/(s/\sqrt(n))\) values are within 0.67 of \(0\).

Constructing Confidence Intervals

According to the \(t\)-distribution:
  • 50% of possible \(t = (\bar{y}-\mu)/(s/\sqrt(n))\) values are within 0.67 of \(0\).
  • 75% of possible \(t = (\bar{y}-\mu)/(s/\sqrt(n))\) values are within 1.15 of \(0\).

Constructing Confidence Intervals

According to the \(t\)-distribution:
  • 50% of possible \(t = (\bar{y}-\mu)/(s/\sqrt(n))\) values are within 0.67 of \(0\).
  • 75% of possible \(t = (\bar{y}-\mu)/(s/\sqrt(n))\) values are within 1.15 of \(0\).

  • 95% of possible \(t = (\bar{y}-\mu)/(s/\sqrt(n))\) values are within 1.96 of \(0\).

Constructing Confidence Intervals

Generally, C% of the time, \[ \begin{align} 0 - t^\star < \underbrace{\frac{\bar{y}-\mu}{s/\sqrt{n}}}_{t} < 0 + t^\star \end{align} \]

  • But, we aren’t interested in what \(t\) is between, we are interested in what \(\mu\) is between. So, lets rearrange this inequality using our algebra skills…

Constructing Confidence Intervals

Generally, C% of the time, \[ \begin{align} 0 - t^\star < \underbrace{\frac{\bar{y}-\mu}{s/\sqrt{n}}}_{t} < 0 + t^\star \end{align} \]

Rearranging this inequality, we get \[ \begin{align} \bar{y} - t^\star \frac{s}{\sqrt{n}} < \mu < \bar{y} + t^\star \frac{s}{\sqrt{n}} \end{align} \] so that \[ \begin{align} \bar{y} \pm t^\star \frac{s}{\sqrt{n}} \end{align} \] is an interval estimate for \(\mu\).

The \(t\)-Confidence Interval for \(\mu\)

If the normal model is appropriate, a C% confidence interval for \(\mu\) is \[ \begin{align} \bar{y} \pm t^\star \frac{s}{\sqrt{n}} \end{align} \]

Terminology:

  • \(t^\star\) is a multiplier that corresponds with your chosen percentage \(C\).
  • The “\(t^\star \frac{s}{\sqrt{n}}\)” part is referred to as the margin of error.
  • Note: the margin of error is equal to the \(t^\star\) value times the standard error (\(s/\sqrt{n}\)).

The \(t\)-Confidence Interval for \(\mu\)

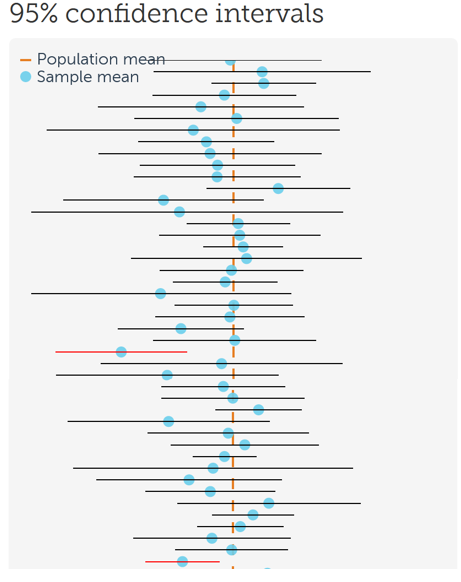
Interpreting a confidence interval:

  • We are C% confident that \(\mu\) is between \(\bar{y}-t^\star\frac{s}{\sqrt{n}}\) and \(\bar{y}+t^\star\frac{s}{\sqrt{n}}\).
  • We have to say “confident” to reflect our belief or uncertainty that \(\mu\) is between \(\bar{y}-t^\star\frac{s}{\sqrt{n}}\) and \(\bar{y}+t^\star\frac{s}{\sqrt{n}}\) (because it might not be).
  • When we say C% confident we mean that, of all possible samples we could get from the population, C% of those samples will give an interval that captures \(\mu\).

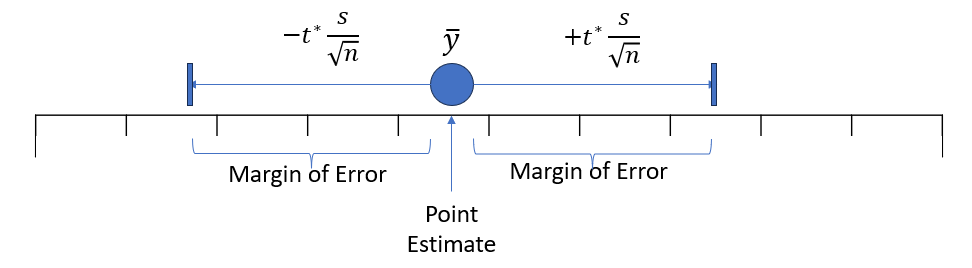
The \(t\)-Confidence Interval for \(\mu\)

Practice 2.4 Question 1

A 95% confidence interval for the average tip amount on rainy days is (18.24, 18.68). Which of the following is a correct interpretation of this interval?

  1. We are 95% sure that the average tip amount on all rainy days is between 18.24 and 18.68.
  2. We are 95% confident that the average tip amount on the observed rainy days is between 18.46 and 18.68.
  3. There is a 95% probability that a tip amount on a rainy day will be between 18.24 and 18.68.
  4. We are 95% confident that the average tip amount on all rainy days is between 18.24 and 18.68.

Practice 2.4 Question 1 Answer

A 95% confidence interval for the average tip amount on rainy days is (18.24, 18.68). Which of the following is a correct interpretation of this interval?

  1. We are 95% sure that the average tip amount on all rainy days is between 18.24 and 18.68.
  2. We are 95% confident that the average tip amount on the observed rainy days is between 18.46 and 18.68.
  3. There is a 95% probability that a tip amount on a rainy day will be between 18.24 and 18.68.
  4. We are 95% confident that the average tip amount on all rainy days is between 18.24 and 18.68.

Example: Santa Claus

What is the average age at which BYU students find out Santa Claus isn’t real? Construct a 99% confidence interval for the average age of all BYU students when they found out the truth about Santa (which we’ll denote by \(\mu\)).

  • Step 1: Collect data (already done)
  • Step 2: Check to make sure I can actually use the \(t\) confidence interval (see if the normal model is appropriate).

Example: Santa Claus

What is the average age at which BYU students find out Santa Claus isn’t real? Construct a 99% confidence interval for the average age of all BYU students when they found out the truth about Santa (which we’ll denote by \(\mu\)).

  • Step 1: Collect data (already done)
  • Step 2: Check to make sure I can actually use the \(t\) confidence interval (see if the normal model is appropriate).
  • Step 3: Have a computer build the confidence interval (I’ll show you how to do this in a minute) \[(8.19, 8.5)\]
  • Step 4: Conclude - We are 99% confident that the average age of all BYU students when they found out Santa wasn’t real is between 8.19 and 8.5.

Example: Chlorine in Swimming Pools

From the previous chlorine analysis, using a 93% confidence interval, help the pool technician determine the average chlorine content across the whole pool.

Step 0 - Open up the course analysis app

Step 1 - Collect data (done)

Step 2 - Check to see if the \(t\)-distribution is appropriate.

Step 3 - Calculate the interval.

Step 4 - Draw conclusions

Using the Tool

Using the Tool

Using the Tool

Example: Chlorine in Swimming Pools

From the previous chlorine analysis, using a 93% confidence interval, help the pool technician determine the average chlorine content across the whole pool.

Step 0 - Open up the course analysis app

Step 1 - Collect data (done)

Step 2 - Check to see if the \(t\)-distribution is appropriate.

  • The density plot (or histogram) was normal.

Step 3 - Calculate the interval.

  • (1.33448, 1.74392)

Step 4 - Draw conclusions

  • We are 93% confident that the average chlorine content across the whole pool is between 1.33 and 1.74.

Practice 2.4 Question 2

From the previous tipping data, is it appropriate to calculate a 90% confidence interval for the average tip amount on all rainy days? Why or why not?

  1. It is NOT appropriate to calculate a CI because the sampling distribution of \(t\) does NOT apply to this particular problem.
  2. It is NOT appropriate because the sampling distribution of \(t\) does apply to this particular problem.
  3. It is appropriate to calculate a CI because the sampling distribution of \(t\) does NOT apply to this particular problem.
  4. It is appropriate to calculate a CI because the sampling distribution of \(t\) does apply to this particular problem.

Practice 2.4 Question 2 Answer

From the previous tipping data, is it appropriate to calculate a 90% confidence interval for the average tip amount on all rainy days? Why or why not?

  1. It is NOT appropriate to calculate a CI because the sampling distribution of \(t\) does NOT apply to this particular problem.
  2. It is NOT appropriate because the sampling distribution of \(t\) does apply to this particular problem.
  3. It is appropriate to calculate a CI because the sampling distribution of \(t\) does NOT apply to this particular problem.
  4. It is appropriate to calculate a CI because the sampling distribution of \(t\) does apply to this particular problem.

Practice 2.4 Question 3

Assuming it is appropriate to calculate a 90% confidence interval, use the 121 analysis tool to find the UPPER bound of a 90% confidence interval for the average tip amount on all rainy days.

Practice 2.4 Question 3 Answer

Assuming it is appropriate to calculate a 90% confidence interval, use the 121 analysis tool to find the UPPER bound of a 90% confidence interval for the average tip amount on all rainy days.

  • 18.277, 18.65

Nuances of Confidence Intervals

What do we do if the sampling distribution of \(t\) doesn’t apply (most likely because the normal population model doesn’t apply)?

If the normal population model is not appropriate BUT you have a large sample size, the sampling distribution of \(t\) is still approximately a \(t\)-distribution with center \(0\), spread \(1\) and degrees of freedom \(n-1\).

Remember: The farther away from a normal model you are, the larger the sample size you will need in order to use the \(t\)-distribution.

Nuances of Confidence Intervals

Confidence Level & Margin of Error

  • Confidence level = the % confident you want to be
  • Margin of Error = \(t^\star \frac{s}{\sqrt{n}}\) = amount above and below point estimate we think \(\mu\) might be

Important relations:

  • As confidence level increases so does margin of error (size of the interval is larger)
  • A 100% confidence interval is \((-\infty, \infty)\).
  • As sample size goes up, margin of error goes down (good thing)
  • Choose confidence level to balance width and confidence in the interval (95% is actually a pretty good balance most of the time)

Practice 2.4 Question 4

Suppose the restaurant owner in the Tipping example continues to collect data on the tip amounts on rainy days and then recalculates the interval including this new data as well as the old data. How will this new 90% confidence interval compare to the old 90% interval (assuming the standard deviations stay the same)?

  1. Stay the same
  2. Narrower
  3. Wider

Practice 2.4 Question 4 Answer

Suppose the restaurant owner in the Tipping example continues to collect data on the tip amounts on rainy days and then recalculates the interval including this new data as well as the old data. How will this new 90% confidence interval compare to the old 90% interval (assuming the standard deviations stay the same)?

  1. Stay the same
  2. Narrower
  3. Wider

Nuances of Confidence Intervals

Confidence Intervals
  • Give a range of reasonable values for the parameter
  • Useful if you don’t have a hypothesis
  • Useful if you are trying to estimate the parameter value
Hypothesis Tests
  • A single conclusion about the validity of a hypothesis.
  • Commonly used to assess a “difference” or an “effect”.
  • Answers yes/no questions about the population

Nuances of Confidence Intervals

Connection: You can use a CI to perform a 2-sided Hypothesis Test

Example: A 99% confidence interval for the average age at which all BYU students learn the truth about Santa Claus is 8.19 and 8.5.

  • Based on this interval, can we say that \(\mu\) is different than 9.5? Why or why not?
  • Based on this interval, can we say that \(\mu\) is different than 8.4? Why or why not?

Nuances of Confidence Intervals

Connection: You can use a CI to perform a 2-sided Hypothesis Test

Example: A 99% confidence interval for the average age at which all BYU students learn the truth about Santa Claus is 8.19 and 8.5.

  • Based on this interval, can we say that \(\mu\) is different than 9.5?
    • Yes because 9.5 is not in the interval
  • Based on this interval, can we say that \(\mu\) is different than 8.4?
    • No because it is in the interval.
  • Rules: A C% CI corresponds to a two-sided hypothesis test using \(\alpha = (1-C/100)\) (for example, 95% and 0.05 or 90% and 0.1)

Practice 2.4 Question 5

Recall from the Chlorine example that the pool technician will add chlorine to the pool if the levels are less than 2ppm. For this analysis, the pool technician should probably use which statistical method:

  1. Point Estimate
  2. Hypothesis Test
  3. Confidence Interval

Practice 2.4 Question 5 Answer

Recall from the Chlorine example that the pool technician will add chlorine to the pool if the levels are less than 2ppm. For this analysis, the pool technician should probably use which statistical method:

  1. Point Estimate
  2. Hypothesis Test
  3. Confidence Interval

Practice 2.4 Question 6

Suppose several days after adding chlorine to the pool, the technician now wants to estimate the average chlorine content across the whole pool. For this analysis, the pool technician should probably use which statistical method:

  1. Point Estimate
  2. Hypothesis Test
  3. Confidence Interval

Practice 2.4 Question 6 Answer

Suppose several days after adding chlorine to the pool, the technician now wants to estimate the average chlorine content across the whole pool. For this analysis, the pool technician should probably use which statistical method:

  1. Point Estimate
  2. Hypothesis Test
  3. Confidence Interval

Key Terminology

  • \(t\)-confidence interval
  • confidence level
  • margin of error
  • confident
  • relationship between hypothesis testing and CIs