Hypothesis Testing for Univariate Quantitative Data

Reminder

Identify population and parameter you are interested in.
- Question: What is the average age at which BYU students find out Santa Claus isn’t real? Specifically, is the average age at which BYU students find out Santa isn’t real older than 8?
- Parameter: The mean age at which all BYU students find out Santa Claus isn’t real. We’ll use the Greek letter \(\mu\) to denote this value.
Collect data
- A convenience sample of 1727 BYU students who are in my class and completed the student survey.
Posit a statistical model based on information in the sample
- Explore the data.
- Posited a normal population model.
Draw inference about the population using your model.

Types of Statistical Inference

3 ways of using sample to make inference about the population:

Point Estimation
Hypothesis Testing
Confidence Intervals (next set of lecture notes)

Point Estimation

Point estimation is a one number estimate of the population parameter.

Our model is \[ \begin{align} Y \sim N(\mu, \sigma) \end{align} \] with population parameters \(\mu\) (a mean) and \(\sigma\) (a standard deviation).

Use sample statistics as estimates of population parameters:

\(\bar{y} \rightarrow \mu\)
\(s \rightarrow \sigma\)

Practice 2.3 Question 1

Using your tipping data, what is the point estimate for the population mean of ALL tip amounts on rainy days?

Practice 2.3 Question 1 Answer

Using your tipping data, what is the point estimate for the population mean of ALL tip amounts on rainy days?

\(\bar{y}\) = 18.464

Law of Large Numbers

How good of an estimate is \(\bar{y}\) to \(\mu\)?

As the sample size (\(n\)) gets bigger, the probability of \(\bar{y}\) being close to \(\mu\) goes up.

Point Estimation

The Good

It’s simple to wrap your head around

The Bad

It’s always wrong (unless you sample the whole population)
If the sample size is small (relative to the size of the population), it could be very wrong.
If there is a lot of variability in the population, it could be very wrong.

Conclusion

While useful, point estimation falls short so lets use a different method to draw conclusions about the population.

Hypothesis Testing

Intuition: Someone makes a claim about a parameter that you assume to be true until your data proves otherwise.

Example: A student claims that the average age BYU students learn about Santa is 8. I believe it may be older than that so I collect data to see if sample data is congruent with the student’s claim.

Hypothesis Testing

Step 1 - Form null and alternative hypotheses:

Null hypothesis: The claim about the parameter that we assume true. This is always a claim of equality. Denoted by \(H_0\).
Alternative hypothesis: The counter-claim that coincides with our beliefs about the parameter. Denoted by \(H_a\).

Hypothesis Testing: Step 1

A student claims that the average age BYU students learn about Santa is 8. I believe it may be older than that so I collect data to see if sample data is congruent with the student’s claim. Write out the null and alternative hypotheses for this research scenario. \[ \begin{align} H_0: \mu &= 8 \\ H_a: \mu &> 8 \end{align} \] Note the following:

Hypotheses are written in terms of the parameter \(\mu\).
Null hypotheses are written with equality.
Alternative hypotheses can be either greater (\(>\)), less (\(<\)) or not equal to (\(\neq\)) - depending on the counter-claim.

Practice 2.3 Question 2

For the tipping scenario, the restaurant manager believes that the average tip on rainy days is different than the average tip amount of 18% on sunny days. How would you write out the null and alternative hypotheses in this scenario?

Practice 2.3 Question 2 Answer

Hypothesis Testing

Step 2 - gather the data and see if our sample data matches (or doesn’t match) the null hypothesis. \[ \begin{align} H_0: \mu &= 8 \\ H_a: \mu &> 8 \end{align} \]

Hypothetical: What if our sample has \(\bar{y} = 8.1\)? Is 8.1 far enough away from 8 to say \(\mu\) > 8? What about \(\bar{y} = 8.2\)? How about \(\bar{y} = 9\)?

What is “different enough” from the null hypothesis to make us think the null is wrong?

We need (1) a measure of how different our sample statistic is from the hypothesized parameter and (2) is the observed difference reasonable to see when sampling from the population.

Consider each of these in turn…

Standardizing Revisited

Measuring the difference between our sample and a hypothesized value:

Note: We’ll use standardized differences because its a common scale for ALL problems.

Recall: to standardize a value is to calculate the number of standard deviations away from the mean a value is using the formula: \[ \begin{align} z = \frac{Y - \mu}{\sigma} = \frac{\text{value} - \text{mean}}{\text{std. dev.}} \end{align} \]

Standardizing Revisited

Measuring the difference between our sample and a hypothesized value:

Note: We’ll use standardized differences because its a common scale for ALL problems.

To standardize a statistic is to calculate the number of standard deviations a statistic is away from a hypothesized value using the formula: \[ \begin{align} t = \frac{\bar{y} - \mu}{s/\sqrt{n}} = \frac{\text{sample mean} - \text{hyp. mean}}{\text{std. error}} \end{align} \]

Key Points

\[ \begin{align} t = \frac{\bar{y} - \mu}{s/\sqrt{n}} = \frac{\text{sample mean} - \text{hyp. mean}}{\text{std. error}} = \frac{8.34 - 8}{2.49/ \sqrt{1727}} = 5.695 \end{align} \]

Because we are standardizing \(\bar{y}\) rather than \(Y\), we use the letter \(t\) instead of \(z\) to highlight the difference.
\(s\) is the standard deviation of individuals (how much \(Y\) could change from individual to individual), but \(s/\sqrt{n}\) is called the standard error of \(\bar{y}\) and measures the standard deviation of \(\bar{y}\) (how much \(\bar{y}\) could change from sample to sample)
We interpret \(t\) similar to \(z\) by saying “our \(\bar{y}\) is \(t\) standard errors away from the hypothesized value.” Example, our sample mean of \(\bar{y}\) = 8.34 is \(t\) = 5.695 standard errors away from the hypothesized mean.

Practice 2.3 Question 3

Practice 2.3 Question 3 Answer

How many standard errors away from the hypothesized value of \(H_0: \mu = 18\) is the sample mean \(\bar{y}\) in the tipping example? (Hint: use the EDA section of the app to find the information you need to calculate \(t\)) \[ \begin{align} t = \frac{\bar{y}-\mu}{s/\sqrt{n}} = \frac{18.464 - 18}{1.101/\sqrt{96}} = 4.126 \end{align} \]

Sampling Distributions

Now that we have a measure of how different our sample is from the hypothesized value, is this difference “different enough” from \(H_0\) for us to no longer believe \(H_0\)?

Definition: A sampling distribution of a statistic is the possible values of that statistic you could observe when you sample from the population AND how often you will observe those values.

Example: The sampling distribution of \(t\) is possible values of \(t\) that we could see when sampling from the population and how often we will see them (if we did repeated sampling).

Sampling Distribution of \(t\)

What the theorem says:

If the normal population model is appropriate and the null hypothesis \(H_0: \mu = \mu_0\) is true, then \[ t = \frac{\bar{y} - \mu_0}{s/\sqrt{n}} \] is a standardized statistic and its sampling distribution is a \(t\)-distribution with center \(0\), spread \(1\) and degrees of freedom \(n-1\) where \(n\) is the size of the sample.

Lets think about this theorem more intuitively!

Sampling Distribution of \(t\)

If the normal population model is appropriate and we have a claim (the null hypothesis) about the mean \(\mu\), then reasonable values of \(t\) that we could see if that null hypothesis is true follow this distribution:

Key Points to Remember

The sampling distribution of \(t\) tells us what values of \(t\) are compatible with \(H_0\) (what values of \(t\) we could get if \(H_0\) is true when we sample from the population).

The normal population model must be appropriate for this sampling distribution to be true.

How can we possibly know what values of \(t\) could happen if only ever take one sample?

Given a population model, we can do math OR computer simulation!

Practice 2.3 Question 4

Is the use of the \(t\) sampling distribution appropriate for the Tipping dataset? (hint: what was the skewness rule of thumb for the normal model?)

Yes because the normal population model applies to this problem
Yes because the normal population model does NOT apply to this problem
No because the normal population model applies to this problem
No because the normal population model does NOT apply to this problem

Practice 2.3 Question 4 Answer

Is the use of the \(t\) sampling distribution appropriate for the Tipping dataset? (hint: what was the skewness rule of thumb for the normal model?)

Yes because the normal population model applies to this problem
Yes because the normal population model does NOT apply to this problem
No because the normal population model applies to this problem
No because the normal population model does NOT apply to this problem

Hypothesis Testing

Revisiting measuring the difference between our sample and a hypothesize value:

Standardized test statistic: the number of standard errors away from the hypothesized value our data is \[ \begin{align} t = \frac{\text{value} - \text{mean}}{\text{std. error of value}} = \frac{\bar{y} - \mu_0}{s/\sqrt{n}} = \frac{8.34 - 8}{2.49/ \sqrt{1727}} = 5.695 \end{align} \]

Hypothesis Testing

To measure if our data is consistent with the null hypothesis:

\(p\)-value: probability of observing our sample result or “more extreme” (as stated by \(H_a\)) if the null hypothesis is true.

The \(p\)-value in our Santa example is the probability of observing \(t\) > 5.695 (because \(H_a: \mu\) > 8) assuming \(\mu = 8\) (which is the null hypothesis).

In our example the \(p\)-value is 0.

Drawing Conclusions

If \(t\) is large then we reject \(H_0\) and conclude that the data support \(H_a\).

If \(p\)-value is small then we reject \(H_0\) and conclude that the data support \(H_a\).

How large is “large enough” or how small is “small enough” for us to reject \(H_0\)?

It depends! We’ll revisit this in a minute but, for now, lets just say if the \(p\)-value is less than 0.05 we’ll reject \(H_0\).

In our Santa example, the \(p\)-value \(=\) 0 which is small. We conclude that our data is NOT consistent with the null hypothesis and that the mean is greater than 8.

Practice 2.3 Question 5

The \(p\)-value from the Tipping example with \[ \begin{align} H_0: \mu &= 18 \\ H_a: \mu &\neq 18 \end{align} \] is 0. Based on the data we collected, what is our conclusion about the average of all tip amounts on rainy days?

Fail to reject the null hypothesis and conclude that the average tip amount on rainy days is equal to 18.
Fail to reject the null hypothesis and conclude that the average tip amount on rainy days is different than 18.
Reject the null hypothesis and conclude that the average tip amount on rainy days is equal to 18.
Reject the null hypothesis and conclude that the average tip amount on rainy days is different than 18.

Practice 2.3 Question 5 Answer

Fail to reject the null hypothesis and conclude that the average tip amount on rainy days is equal to 18.
Fail to reject the null hypothesis and conclude that the average tip amount on rainy days is different than 18.
Reject the null hypothesis and conclude that the average tip amount on rainy days is equal to 18.
Reject the null hypothesis and conclude that the average tip amount on rainy days is different than 18.

Example: Chlorine in Swimming Pools

Lets put it all together using another example…

Chlorine is often used to eliminate bacteria and algae by disinfecting (killing) pool water while also oxidizes (chemically destroys) other materials such as dirt and chloramines. Adding the right amount of chlorine is sometimes a tough balancing act, but it is absolutely necessary to maintaining a healthy pool. On the one hand, not enough chlorine will not properly disinfect the water. On the other, too much chlorine can cause sickness and injuries, including rashes, coughing, nose or throat pain, eye irritation and bouts of asthma. A “safe” level of chlorine could be between 2ppm and 3ppm.

A pool technician takes regular measurements of the chlorine content in the water to ensure appropriate chlorine content. The Chlorine dataset (on the course analysis app) is a sample of chlorine content at 30 different locations in a public pool. The technician likes to keep the chlorine levels at about 2ppm and thinks the water is about that level. However, after swimming in the pool, you feel a little nauseous and think it might be lower. Carry out a test to see if you are correct.

Example: Chlorine in Swimming Pools

Step 0 - Open up the course analysis app

Step 1 - Write out the hypotheses.

Let \(\mu\) represent the mean chlorine content across the pool. Fill in the appropriate hypotheses: \[ \begin{align} H_0: \\ H_a: \\ \end{align} \]

Step 2 - Collect data and see if the data is consistent with \(H_0\).

Make sure to check if the \(t\)-distribution is appropriate in doing this.

Step 3 - Draw a conclusion.

Using the Online Tool

Example: Chlorine in Swimming Pools

Step 0 - Open up the course analysis app

Step 1 - Write out the hypotheses.

Let \(\mu\) represent the mean chlorine content across the pool. Fill in the appropriate hypotheses: \[ \begin{align} H_0: \mu = 2\\ H_a: \mu < 2\\ \end{align} \]

Example: Chlorine in Swimming Pools

Step 2 - Collect data and see if the data is consistent with \(H_0\).

\(t\)-distribution is appropriate.
\(t=-4.23\)
\(p\)-value \(=0.0001\)

Step 3 - Draw a conclusion.

Our data is not consistent with the null hypothesis so we conclude that the mean content is less than 2.

Nuances of Hypothesis Testing

What do we do if the sampling distribution of \(t\) doesn’t apply (which we be because the normal population model doesn’t apply to our problem)?

Key Issue: If the sampling distribution of \(t\) doesn’t apply to our problem, then we can’t use it to calculate a \(p\)-value.

Solution -

If the normal model is not appropriate BUT you have a large sample size, the distribution of \(t\) is still approximately a \(t\)-distribution with center \(0\), spread \(1\) and degrees of freedom \(n-1\).

Nuances of Hypothesis Testing

What do we do if the sampling distribution of \(t\) doesn’t apply (which we be because the normal population model doesn’t apply to our problem)?

Even if the normal model doesn’t perfectly apply, using the sampling distribution of \(t\) is still OK if we have a large sample size according to the central limit theorem.

What is a “large” sample size?
It depends! If you have strong skewness or big outliers then you need a bigger sample size.
\(n > 30\) is usually a pretty good “rule-of-thumb” and we’ll use this for this class.
See the Central Limit Theorem part of the course analysis app

Nuances of Hypothesis Testing

What is “small” for a \(p\)-value? In other words, what cutoff should I use for my \(p\)-value to make conclusions?

Key Issue: what we define as “small” dictates whether we feel our data is consistent with the null hypothesis or not.

Solution: Choose a cutoff value for the \(p\)-value (called a significance level) between 0 and 1 that takes into account consequences of making a mistake in your conclusions (errors in hypothesis testing).

Errors in Hypothesis Testing

Example: You take a COVID test with \[ \begin{align} H_0&: \text{You are negative} \\ H_a&: \text{You are positive} \end{align} \]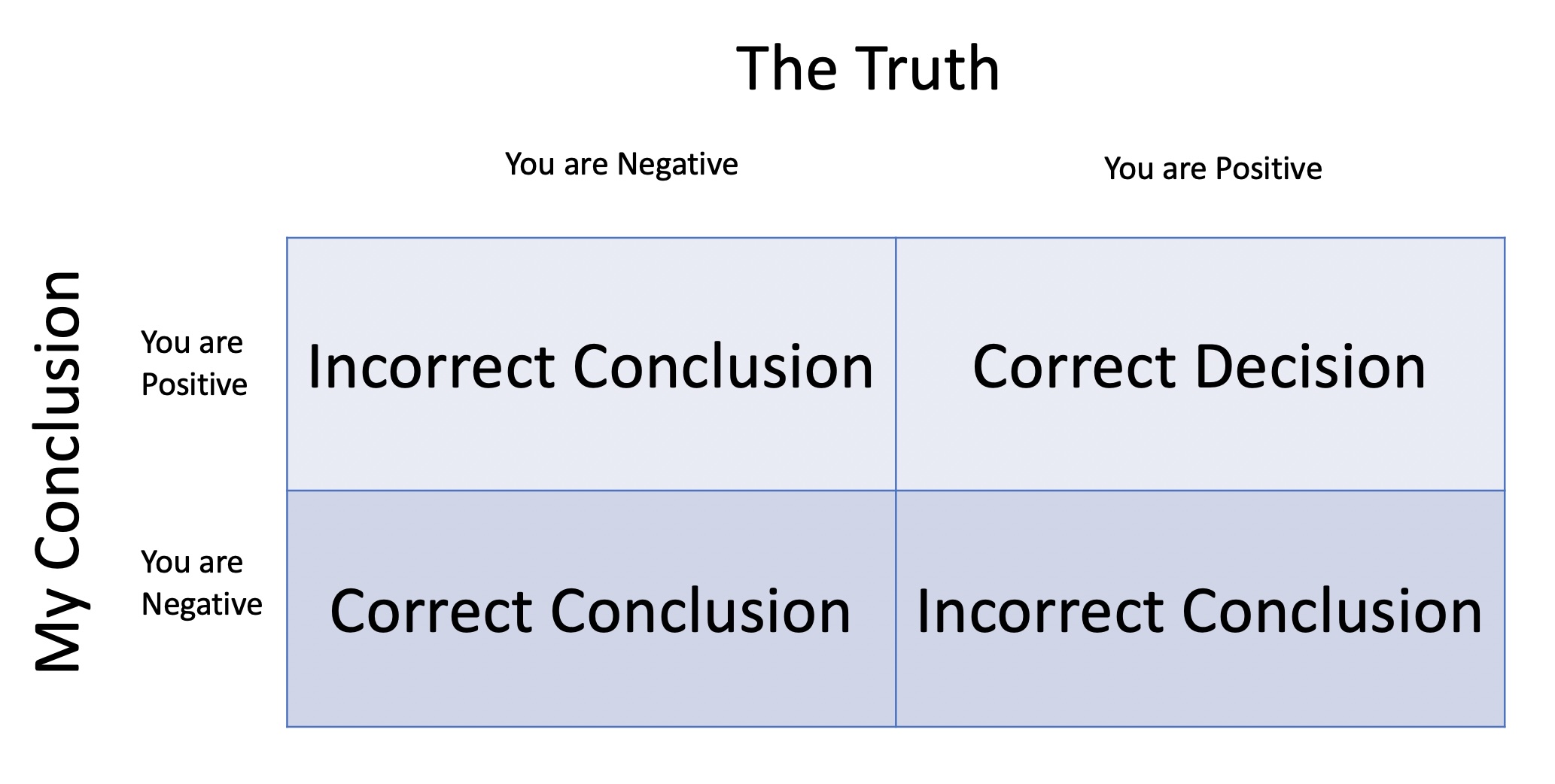

Errors in Hypothesis Testing

Type 1 Error = rejecting \(H_0\) when you shouldn’t
- What would a Type 1 error be for COVID example?
- What would it be for Santa example?
Type 2 Error = failing to reject the \(H_0\) when you should reject \(H_0\)
- What would a Type 2 error be for COVID example?
- What would it be for Santa example?

Errors in HT - Terminology

Significance level (denoted by \(\alpha\)) - your \(p\)-value “cutoff” and the probability of a Type 1 Error if null is true (a bad thing).
Power of a test - the probability that you reject the null hypothesis when the null hypothesis is wrong (a good thing).

Issue: the significance level and power work against each other.

If you decrease the probability of a Type 1 Error (\(\alpha\)), you also decrease the power because its harder to find data NOT consistent with \(H_0\).

Nuances of Hypothesis Testing

What is “small” for a \(p\)-value? In other words, what cutoff should I use for my \(p\)-value to make conclusions?

It depends!

If Type 1 error is a big deal then set \(\alpha\) small.
If Type 1 error is not a big deal then set \(\alpha\) bigger.
Generally, set \(\alpha\) so that it is a good balance between making a mistake (Type 1 Error) and being correct (Power).
- \(\alpha = 0.05\) is usually a pretty good balance

Nuances of Hypothesis Testing

Drawing conclusions.

We assume the null hypothesis is true in order to use the \(t\)-distribution theorem. Therefore:

We either “reject” or “fail to reject” the null hypothesis as our conclusion.
We can never “accept” the null hypothesis.

Nuances of Hypothesis Testing

Statistical vs. practical significance.

Two key definitions:

Statistical significance - you reject \(H_0\).
Practical significance - the difference between your observed result and the hypothesized result is big enough to matter in real life.

Statistical vs. Practical Significance

Example: Researchers are studying a new weight-loss program. Using a large sample they carry out a test of \(H_a: \mu > 0\) where \(\mu\) is the mean weight loss (in pounds) and conclude that their results were statistically significant at the 0.05 \(\alpha\) level. However, the mean weight loss of participants in the study was \(\bar{y} = 0.25\) pounds. Most people would say that the results are not practically significant because a six month weight-loss program should yield a mean weight loss much greater than the one observed in this study.

Lesson: Don’t just look at \(p\)-value \(< \alpha\) to make scientific conclusions. Look at \(\bar{y}\) relative to \(H_0\) as well.

Practice 2.3 Question 6

The tipping example had \(\bar{y}\) = 18.46 and our test had \(p\)-value = \(0.0001\). Using a significance level of \(\alpha = 0.01\), is this test statistically and/or practically significant? Recall that \[ \begin{align} H_0: \mu&= 18 \\ H_A: \mu&\neq 18 \end{align} \]

The test is statistically significant but not practically significant
The test is statistically significant and practically significant
The test is NOT statistically significant and not practically significant
The test is NOT statistically significant but is practically significant

Practice 2.3 Question 6 Answer

The test is statistically significant but not practically significant
The test is statistically significant and practically significant
The test is NOT statistically significant and not practically significant
The test is NOT statistically significant but is practically significant

Practical significance is a subjective judgement call so it could be either depending on your opinion.

Nuances of Hypothesis Testing

The effect of sample size

All else being equal, a bigger sample size means:

\(t\) gets bigger (further from zero)
\(p\)-value gets smaller
easier to reject \(H_0\) (find statistical significance but not necessarily practical significance)

Practice with Hypothesis Testing

I claim that BYU students think BYU was founded in 1900. You think that BYU students know more than that and they know it was founded before 1900. Carry out a hypothesis test to settle the debate.

What are the null and alternative hypothesis?
What does the sampling distribution of \(t\) tell us under the null hypothesis?
Is the \(t\)-distribution appropriate for this problem? Why or why not?
Assuming the \(t\) distribution in OK, what is the \(t\) test statistic? How do we interpret it?
What is the \(p\)-value? How do we interpret it?

Practice Continued

Am I right or are you (use \(\alpha = 0.1\))? Meaning, do we reject \(H_0\) or fail to reject it?
What is a Type 1 error in this case?
What is a Type 2 error in this case?
Should \(\alpha\) be lower or higher in this case?
What is power in this case?
Is the result practically significant? Why or why not?

Practice (Answers)

I claim that BYU students think BYU was founded in 1900. You think that BYU students know more than that and they know it was founded before 1900. Carry out a hypothesis test to settle the debate.

What are the null and alternative hypothesis? \(H_0: \mu = 1900\text{ } H_a:\mu < 1900\)
What does the sampling distribution of \(t\) tell us under the null hypothesis? The possible values of \(t\) that we could get when we sample IF the null hypothesis is true.
Is the \(t\)-distribution appropriate for this problem? Why or why not? The \(t\) distribution is OK because we have a large sample size AND there is not strong skewness.
Assuming the \(t\) distribution in OK, what is the \(t\) test statistic? How do we interpret it? \(t = -6.729\). Our sample mean of 1890.986 is -6.729 standard errors away from the hypothesized value of 1900.
What is the \(p\)-value? How do we interpret it? \(p\)-value = 0; IF the null hypothesis is true, the probability of us seeing \(\bar{y} =\) 1890.986 or less is 0.

Practice (Answers)

Am I right or are you (use \(\alpha = 0.1\))? Meaning, do we reject \(H_0\) or fail to reject it? We reject the null and conclude that students know BYU was founded before 1900.
What is a Type 1 error in this case? Saying that students know BYU was founded before 1900 when they think it was founded about 1900.
What is a Type 2 error in this case? Saying that students think BYU was founded around 1900 when, in fact, they know it was founded before 1900.
Should \(\alpha\) be lower or higher in this case? It depends!
What is power in this case? The probability of concluding that students know it was founded before 1900 when, in fact, they know it was founded before 1900.
Is the result practically significant? Why or why not? Maybe.

Key Terminology

Point Estimation
Hypothesis testing
Law of large numbers
Steps in hypothesis testing
Type 1 Error
Type 2 Error
Power of a test

Errors in hypothesis testing
Test statistics
\(p\)-value
Significance level
Central limit theorem
Statistical significance
Practical significance
\(t\)-distribution
Standard error